CBSE Class 10 Math Question Paper 2016 | Q7

Class 10 Maths Questions

The given question is a medium difficulty 2-mark question from the chapter Circles. Concept tested: Lenghts of tangents drawn to a circle from an external point. The question appeared in the 2016 CBSE class 10 board paper.

Question 7: A quadrilateral ABCD is drawn to circumscribe a circle, with centre 0, in such a way that the sides AB, BC, CD and DA touch the circle at the points P, Q, R and S respectively. Prove that AB + CD = BC + DA

---

Video Explanation

---

---

Explanatory Answer | CBSE 2016 Maths Paper Q7

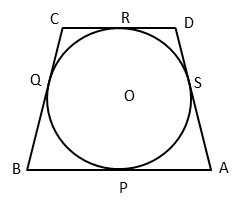
Circle Property
From an external point, two tangents can be drawn to a circle. Both these tangents will be equal in length.

AP and AS are equal tangents drawn from A. Let the measure of AP = AS ='a' units.
BP and BQ are equal tangents drawn from B. Let the measure of BP = BQ = 'b' units.
CQ and CR are equal tangents drawn from C. Let the measure of CQ = CR = 'c' units.
DR and DS are equal tangents drawn from D. Let the measure of DR = DS = 'd' units.

To prove: AB + CD = BC + DA

LHS: AB + CD = AP + PB + CR + RD
= a + b + c + d ............. (1)

RHS: BC + DA = BQ + QC + DS + SA
= b + c + d + a ............. (2)

(1) = (2)

∴ AB + CD = BC + DA