CBSE Class 10 Math Question Paper 2016 | Q10

The given question is a hard 2-mark question from the chapter Circles. It combines multiple concepts. Concept tested: Properties of tangents to a circle, values of trigonometric ratios, and properties of isosceles triangles. It is an important question and appeared in Section B of the 2016 CBSE class 10 board paper.

Question 10: From an external point P, two tangents PT and PS are drawn to a circle with centre O and radius r. If OP = 2r, show that ∠OTS = ∠OST= 30°

Video Explanation

Explanatory Answer | CBSE 2016 Maths Paper Q10

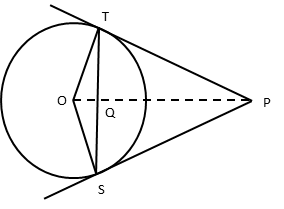
∠OTP = 90° because the angle between a tangent and a radius where the tangent meets the circle is a right angle.
∴ ΔOTP is a right triangle

Step 1: Compute ∠OPT

Sin ∠OPT = \\frac{\text{Opposite side}}{\text{Hypotenuse}}) = \\frac{\text{OT}}{\text{OP}})
OT is a radius to the circle. So, OT = r.
Given Data: OP = 2r.
∴ Sin ∠OPT = \\frac{\text{r}}{\text{2r}}) = \\frac{\text{1}}{\text{2}})
Sin 30° = \\frac{\text{1}}{\text{2}})
∴ ∠OPT = 30°

Step 2: Compute ∠POT

Sum of the interior angles of a triangle = 180°
In Δ OPT, ∠OPT + ∠OTP + ∠POT = 180°
30° + 90° + ∠POT = 180°
Or ∠POT = 60°

Step 3: Compute ∠SOT

By RHS rule Δ OPT and Δ OPS are congruent
∴ ∠QOT = ∠QOS = 60° (∠QOT is the same as ∠POT = 60°)
Hence, ∠SOT = ∠QOT + ∠QOS = 60 + 60 = 120°

Step 4: Prove ∠OTS = ∠OST = 30°

Δ SOT is an isosceles triangle because OS and OT are radii to the circle.
∴ ∠OTS = ∠OST = x

In Δ SOT, ∠SOT + ∠OTS + ∠OST = 180°
120° + x + x = 180°
Or x = 30°
i.e., ∠OTS = ∠OST = 30°