CBSE Class 10 Math Question Paper 2016 | Q11

The given question is a medium difficulty 3-mark question from the chapter Areas Related to Circles. Computing area of a semi circle and area of a right triangle to find the area of a shaded region. It is an important question and appeared in Section C of the 2016 CBSE class 10 board paper.

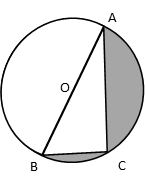
Question 11: O is the centre of a circle such that diameter AB = 13 cm and AC = 12 cm. BC is joined. Find the area of the shaded region. (Take π = 3.14).

Video Explanation

Explanatory Answer | CBSE 2016 Maths Paper Q11

AB is a diameter to the circle.

Property
Angle in a semicircle is a right angle.

∴ ∠ACB = 90°
∴ Δ ACB is a right triangle.

Step 1: Compute length of side BC

By Pythagoras theorem, AB² = AC² + BC²
AB = 13 cm, AC = 12 cm
13² = 12² + BC²
Or BC² = 169 - 144 = 25
∴ BC = 5 cm

Step 2: Compute Area of Shaded Region

Area of shaded region = Area of semicircle of radius \\frac{13}{2})cm - Area of right triangle ACB
Sides of right triangle ACB are 5, 12, and 13.
∴ Area of shaded region = \\frac{1}{2}) × (3.14) × \(\frac{13}{2}{)}^{2}) - \\frac{1}{2}) × 12 × 5
= \\frac{1}{2}) × 3.14 × \\frac{169}{4}) - 30
= \\frac{3.14 × 169-240}{8}) = 36.3325 sq cm