CBSE Class 10 Maths Paper | 2018 Q15B

Question 15B: If A(- 5, 7), B(- 4, - 5), C(- 1, - 6) and D(4, 5) are the vertices of a quadrilateral. Find the area of the quadrilateral ABCD.

Video Explanation

Explanatory Answer | Class 10 Maths 2018 Q15 B

A(-5, 7), B(-4, -5), C(-1, -6) and D(4, 5) are vertices of a quadrilateral.
Join AC. We get 2 triangles ABC and ADC.

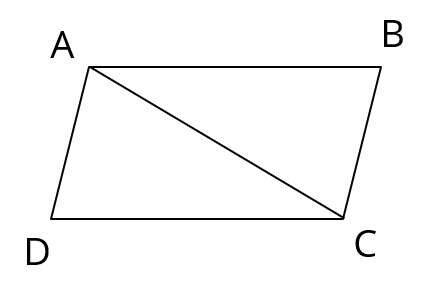
Area of quadrilateral ABCD = Area of ∆ABC + Area of ∆ADC.

Step 1: Compute Area of Triangle ABC

Area of ∆ABC = \\frac{1}{2}) {x₁(y₂ – y₃) + x₂ (y₃ - y₁) + x₃(y₁ – y₂)}
A(-5, 7), B(-4, -5) and C(-1, -6)
Area of ∆ABC = \\frac{1}{2}) {(-5) (-5 – (-6) + (-4) (-6 – 7) + (-1) (7 – (-5))}
Area of ∆ABC = \\frac{1}{2}) {(-5) (1) + -4(-13) + (-1)(12)}
Area of ∆ABC = \\frac{1}{2}) {-5 + 52 – 12} = \\frac{1}{2}) × 35 = 17.5 sq units

Step 2: Compute Area of Triangle ADC

Area of triangle ADC = \\frac{1}{2}) {x₁(y₂ – y₃) + x₂ (y₃ - y₁) + x₃(y₁ – y₂)}
A(-5, 7), C(-1, -6), and D(4, 5)
Area of ∆ADC = \\frac{1}{2}) {(-5)(-6 - 5) + (-1)(5 – 7) + 4(7 – (-6))}
Area of ∆ADC = \\frac{1}{2}) {(-5)(-11) + (-1) (-2) + 4(13)}
Area of ∆ADC = \\frac{1}{2}) {55 + 2 + 52} = \\frac{109}{2}) = 54.5 sq units

Step 3: Compute Area of Quadrilateral ABCD

Area of quadrilateral ABCD = 17.5 + 54.5 = 72 sq units