CBSE Class 10 Maths Question Paper 2018 Solution | Q25A

Question 25A: In an equilateral ∆ABC, D is a point on side BC such BD = \\frac{1}{3})BC. Prove that 9(AD)² = 7(AB)²

Video Explanation

Explanatory Answer | CBSE Class 10 Math Paper 2018 Q25A

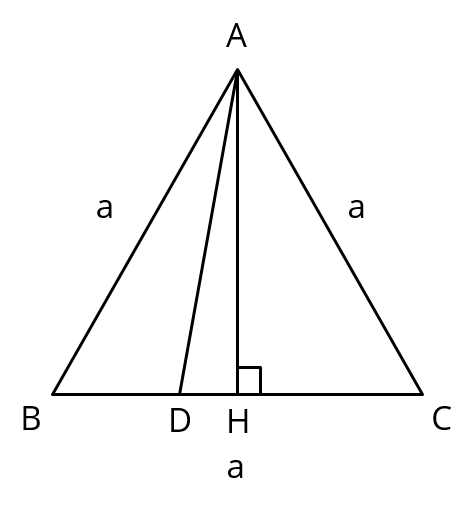
ABC is an equilateral triangle.
BD = \\frac{1}{3}) BC
Let the side of equilateral triangle measure 'a' units.

Draw AH perpendicular to BC.
In right triangle AHC, AH² + HC² = AC²
By SAS rule AHB and AHC are congruent,
HC = \\frac{1}{2}) BC = \\frac{1}{2}) a

In right triangle AHB, AH² = AB² - HB²
AH² = a² - (\\frac{1}{2}) a)² = a² - \\frac{1}{4}) a² = \\frac{3}{4}) a²

In right triangle ADH, AD² = AH² + HD²
HD = BH - BD = \\frac{1}{2})a - \\frac{1}{3})a = \\frac{1}{6})a

∴ AD² = \\frac{3}{4})a² + (\\frac{1}{6})a)² = \\frac{3}{4})a² + \\frac{1}{36})a²
           = \\frac{27a^2 + a^2}{36}) = \\frac{28}{36})a² = \\frac{7}{9})a²

∴ AD² = \\frac{7}{9})(AB)²
or 9(AD)² = 7(AB)²