CBSE Class 10 Math 2018 Question Paper Solution | Q28

This four mark question requires the knowledge of the formula to compute the curved surface area of a the frustum of a cone. A relatively easy question if you know the above mentioned formula.

Question 28: The diameters of the lower and upper ends of a bucket in the form of a frustum of a cone are 10 cm and 30 cm respectively. If its height is 24 cm, find the area of the metal sheet used to make the bucket.

Video Explanation

Explanatory Answer | CBSE Class 10 Math 2018 Paper Question 28

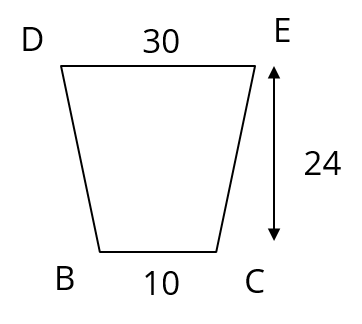
Lower diameter of the bucket = 10 cm. So, lower radius r₂ = 5 cm
Upper diameter of the bucket = 30 cm. So, upper radius r₁ = 15 cm
Height = 24 cm

Area of metal used to make bucket = curved surface area of the frustum of the cone + area of circular base

Step 1: Compute Slant Height of the Frustum of Cone

Curved surface area of frustrum of cone = πl (r₁ + r₂)
where l is the slant height of frustrum = \\sqrt{h^2 + (r_1 - r_2)^2})
Slant Height = \\sqrt{24^2 + (15 - 5)^2}\\) = \\sqrt{24^2 + 10^2}\\) = \\sqrt{576 + 100}\\) = \\sqrt{676}\\) = 26

Step 2: Compute Curved Surface Area of Frustum of Cone and Area of Circular Base

Curved surface area of cone = π × 26 × (15 + 5) = 520π
Area of circular base = π(5)² = 25π

∴ Area of metal sheet required = 520π + 25π = 545π
= 545 × 3.14
= 1711.3 sq cm