Question: The diagonal of a rectangular field is 60 metres more than the shorter side. If the longer side is 30 metres more than the shorter side, find the sides of the field.
Video Explanation
Explanatory Answer
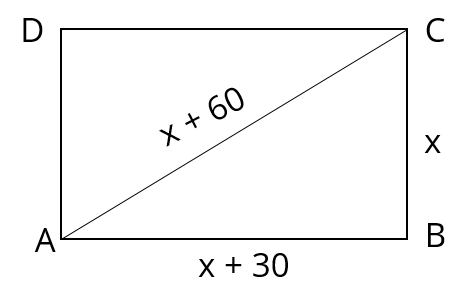
Let the shorter side BC measure x units.
The diagonal is 60 metres more than the shorter side.
So, diagonal AC = x + 60
Length is 30 metres more than the shorter side.
So, length AB = x + 30
In right triangle, ABC, AC2 = AB2 + BC2
So, (x + 60)2 = (x + 30)2 + x2
x2 + 120x + 3600 = x2 + 60x + 900 + x2
x2 – 60x – 2700 = 0
Factorize the equation to find x
x2 – 90x + 30x – 2700 = 0
x(x – 90) + 30(x – 90) = 0
(x – 90)(x + 30) = 0
x = 90 and x = -30.
'x' is the measure of the shorter side of the rectangle.
The measure of the shorter side cannot be negative.
Therefore, shorter side measures 90 m.
Measure of longer side = x + 30 = 90 + 30 = 120 m
