2019 CBSE Class 10 Maths Sample Question Paper | 4 Mark Question Solution & Videos

Section D contains 8 questions of 4 marks each. Scroll down for explanatory answer and video solution to the 4-mark questions that appeared in Class 10 Maths CBSE board exam in 2019. Questions appeared from the following chapter : Quadratic Equations, Arithmetic Progressions, Triangles, Trigonometry, Surface Areas & Volumes, Applications of Trigonometry, and Statistics.

Question 23 | Internal Choice A

A train takes 2 hours less for a journey of 300 km if its speed is increased by 5 km/h from its usual speed. Find the usual speed of the train.

How to solve this Quadratic Equations word problem?

Step 1: Assign a variable for the usual speed of the train.
Step 2: Frame an equation each for time taken to cover 300 km at s km/hr and (s + 5) km/hr respectively.
Step 3: Simplify the two equations to get a quadratic equation in 's'.
Step 4: Solve for s to arrive at the answer.

OR

Question 23 | Internal Choice B

Solve for x: \\frac{1}{(a + b + x)}) = \\frac{1}{a}) + \\frac{1}{b}) + \\frac{1}{x}) , [a ≠ 0, b ≠ 0, x ≠ 0, x ≠ -(a + b)]

Approach to solve this Quadratic Equations problem

Step 1: Take LCM of denominators on both sides of the equation.
Step 2: Cross multiply to get a quadratic equation in x.
Step 3: Factorize the quadratic equation to find two answers for x.
Question 24

An AP consists of 50 terms of which 3rd term is 12 and the last term is 106. Find the 29th term.

How to solve this Arithmetic Progressions question?

Concept: The formula to find the n^th term of an AP is a_n = a + (n - 1)d, where a is the first term, n is the number of terms, and d is the common difference of the AP.
Step 1: Express the third term in terms of the first term of the AP and the common difference. Call it equation (1).
Step 2: Express the 50^th term in terms of the first term and the common difference. Call it equation (2).
Step 3: Solve equations (1) and (2) to find the value of d.
Step 4: Substitute the value of 'd' in one of the two equations to find 'a'.
Step 5: Compute the value of the 29th term using the values of a and d computed in steps 3 and 4.
Question 25

Prove that in a right angled triangle square of the hypotenuse is equal to sum of the squares of other two sides.

Hint to solve this Triangles problem

Concept: Proving the Pythagoras Theorem.
Theorem: If a perpendicular is drawn from the vertex of the right angle of a right triangle to the hypotenuse then triangles on both sides of the perpendicular are similar to the whole triangle and to each other.
Step 3: Draw a right triangle ABC right angled at B. Draw BD ⊥ AC
Step 4: From the theorem, ΔADB ~ ΔABC and ΔBDC ∼ ΔABC (Theorem)
Step 5: Therefore, \\frac{AD}{AB}) = \\frac{AB}{AC}) and \\frac{CD}{BC}) = \\frac{BC}{AC})
Step 6: Solve the above equations and add them to prove Pythagoras Theorem.

Question 27 | Internal Choice A

A man on the top of a vertical observation tower observes a car moving at a uniform speed coming directly towards it. If it takes 12 minutes for the angle of depression to change from 30° to 45°, how long will the car take to reach the observation tower from this point?

Hint to solve this Applications of Trigonometry problem

Step 1: Apply tan 45 in triangle ACD and establish that CD = AD.
Step 2: Apply tan 30 in triangle ABD and compute BC in terms of CD.
Step 3: It takes 12 seconds to cover BC. So, compute time taken to cover CD.

OR

Question 27 | Internal Choice B

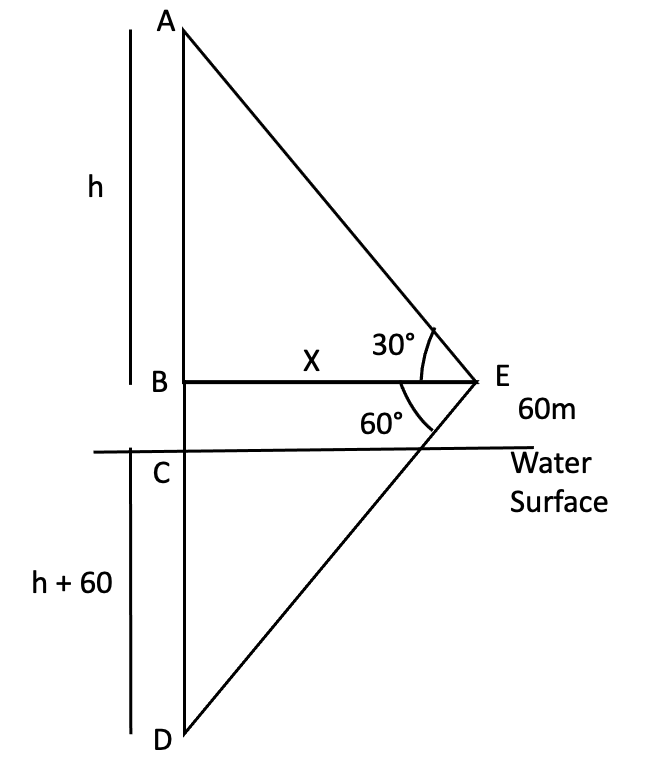
The angle of elevation of a cloud from a point 60 m above the surface of the water of a lake is 30° and the angle of depression of its shadow from the same point in water of lake is 60°. Find the height of the cloud from the surface of water.

Approach to prove Applications of Trigonometry problem

Step 1: In triangle ABE, find tan of angle of elevation and express BE in terms of height of the cloud.
Step 2: In triangle BDE, compute tan 60 and compute h after substituting BE in terms of h.
Question 28 | Internal Choice A

The median of the following data is 525. Find the values of x and y if the total frequency is 100.

Class Interval Frequency Class Interval Frequency

0-100 2 500-600 20

100-200 5 600-700 y

200-300 x 700 – 800 9

300-400 12 800-900 7

400-500 17 900-1000 4

Hint to solve this Statistics problem

Step 1: Identify the median class and substitute values in the median formula for grouped data.
Step 2: Solve the equation by substituting median as 525 and compute value for x.
Step 3: Substitute value of x and compute value of y.

OR

The following data indicates the marks of 53 students in Mathematics. Draw less than type ogive for the data and hence find the median.

Marks No.of.students Marks No.of.students

0-10 5 50-60 4

10-20 3 60-70 7

20-30 4 70 – 80 9

30-40 3 80-90 7

40-50 4 90-100 8

Approach to solve this Statistics problem

Step 1: Compute cumulative frequency table from grouped data for less than the upper limit of each class interval.
Step 2: Draw the less than type ogive with the upper limit as the x-axis and the cumulative frequency as the y-axis.
Step 3: Drop a perpendicular at the point where the cumulative frequency is 27 (54/2) and find the value on the x-axis where the perpendicular meets the x-axis to compute the median.
Question 29

The radii of the circular ends of a bucket of height 24 cm are 15 cm and 5 cm. Find the area of its curved surface.

Hint to solve this Surface Areas problem

Formulae Used: CSA of frustum of cone = π × (R + r) × l, where R and r are the radii of the top and bottom of the frustum of the cone and l is the slant height.
Step 1: Compute slant height using Pythagoras Theorem.
Step 2: Compute CSA of frustum of cone using the radii of the top and bottom of the bucket and the slant height computed in step 1.
Question 30

If sec θ + tan θ = p, then find the value of cosec θ.

Hint to solve this Trigonometry problem

Step 1: Rewrite sec θ and tan θ in terms of sin θ and cos θ
Step 2: Express cos θ = \\sqrt{1 – {sin}^{2}θ})
Step 3: Square both sides of the equation. Will result in a quadratic equation with sin θ being the variable.
Step 4: Solve the quadratic equation for sin θ using the quadratic formula.
Step 5: The reciprocal of the values obtained for sin θ are the answers to the question asked.