CBSE Class 10 Maths 2019 Sample Question Paper

Section A contains 6 questions of 1 mark each. Scroll down for explanatory answer and video solution for all six one mark questions. Questions appeared from Quadratic Equations, Real Numbers, Coordinate Geometry, Arithmetic Progressions, Trigonometry, and Triangles.

1. Question 1

   Find the value of a, for which point P(\\frac{a}{3}) , 2) is the mid-point of the line segment joining the points Q(-5,4) and R(-1,0).

   Hint to solve this Coordinate Geometry question

   Substitute the coordinate of the points Q and R in the midpoint formula and solve it to find the value for a.

   Explanation Video Solution Coordinate Geometry

   ---

2. Question 2 | Internal Choice A

   Find the value of k, for which one root of the quadratic equation kx² - 14x + 8 = 0 is 2.

   Hint to solve this Quadratic equations question

   One of the roots of the equation is 2. So, substituting x = 2 will satisfy the equation. By substituting the value of x as 2, we can find the value of k.

   Explanation Video Solution Quadratic Equations
   OR

   Question 2 | Internal Choice B

   Find the value(s) of k for which the equation x² + 5kx + 16 = 0 has real and equal roots.

   Hint to solve this Quadratic equations question

   Roots of the quadratic equation are real and equal.
   
   If the roots are real and equal, the discriminant (D) of the equation is 0.
   
   Express discriminant b² - 4ac in terms of k and equate it to zero to compute the value of k.

   Explanation Video Solution Quadratic Equations

   ---

3. Question 3 | Internal Choice A

   Write the value of cot²θ − \\frac{1}{sin^2θ})

   Hint to solve this Trignometric Identities Question

   Step 1:Express cot θ in terms of cos θ and sin θ
   Step 2: The denominator of both the terms of the expression will become sin² θ
   Step 3>: Simplify the numerator and cancel like terms in the numerator and denominator to find the value of the expression.

   Explanation Video Solution Trigonometry
   OR

   Question 3 | Internal Choice B

   If sin θ = cos θ, then find the value of 2 tanθ + cos² θ

   Hint to solve this Trignometric Ratios Question

   Step 1: Compute value of θ for which sin θ = cos θ
   Step 2: Substitute value of θ computed in step 1 into the given expression to find the value of the expression.

   Explanation Video Solution Trigonometry

   ---

4. Question 4

   If n^th term of an A.P. is (2n + 1), what is the sum of its first three terms?

   Hint to solve this CBSE 2019 sample paper 1 mark Arithmetic Progressions problem

   Approach: Compute the 1st, 2nd, and 3rd term by susbtituting n = 1, n = 2, and n = 3 in the expression (2n + 1). Subsequently, find the sum of the 3 terms.
   

   Explanation Video Solution Arithmetic Progressions

   ---

5. Question 5

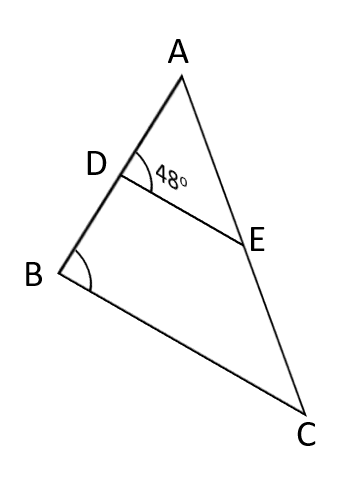
   In figure if AD = 6cm, DB = 9cm, AE = 8cm and EC = 12cm and ∠ADE = 48°. Find ∠ABC.

   Hint to solve this CBSE 2019 sample paper 1 mark Triangles question

   Concept: Check whether Basic Proportionality theorem applies in this case.
   Step 1: Compute ratio between AD and DB and between AE and EC
   Step 2: If the ratios are same, by converse of Basic Proportionality Theorem, DE will be parallel to BC.
   Step 3: If DE is parallel to BC, corresponding angles will be equal and the answer can be computed.

   Explanation Video Solution Triangles

   ---

6. Question 6

   After how many decimal places will the decimal expansion of \\frac{23}{2^4 × 5^3}) terminate?

   Hint to solve this CBSE 2019 sample paper 1 mark Real Numbers question

   Step 1: Rewrite the fraction such that the powers of 2s and 5s in the denominator is the same. This ensures that we get the denominator as a power of 10
   Step 2: The power of 10 in the denominator is the number of decimal places in the decimal expansion of the fraction.

   Explanation Video Solution Real Numbers

   ---

Video Solution and Explanatory Answers to CBSE 2019 Sample Paper - 1 mark questions 1 to 6

Question 1: Find the value of a, for which point P(\\frac{a}{3}) , 2) is the mid-point of the line segment joining the points Q(-5,4) and R(-1,0).

Q1 Video Explanation

Scroll down further for explanatory answer text

---

Explanatory Answer | Q1 2019 Sample Question Paper

Midpoint of 2 points (x₁, y₁) and (x₂, y₂) = \\frac{x_1 + x_2}{2}), \\frac{y_1 + y_2}{2})
The points given here are Q(-5, 4) and R(-1, 0) and the midpoint is P(\\frac{a}{3}), 2)
∴\\frac{-5 + (-1)}{2}) = \\frac{a}{3}) and \\frac{4 + 0}{2}) = 2
\\frac{-6}{2}) = \\frac{a}{3})
a = -9

---

Question 2: Find the value of k, for which one root of the quadratic equation kx² - 14x + 8 = 0 is 2.

Q2 Internal Choice 1 Video Explanation

Scroll down further for explanatory answer text

---

Explanatory Answer | Q2 Internal Choice 1

If 2 is one of the roots of the quadratic equation kx² - 14x + 8 = 0, then it will satisfy the equation
Substitute x = 2 in the above equation.
∴ k(2)² – 14(2) + 8 = 0
4k – 28 + 8 = 0
4k = 20
k = 5

OR

Question 2 Internal Choice 2: Find the value(s) of k for which the equation x² + 5kx + 16 = 0 has real and equal roots.

Q2 Internal Choice 2 Video Explanation

Scroll down further for explanatory answer text

---

Explanatory Answer | Q2 Internal Choice 2

If a quadratic equation has real and equal roots, then the discriminant (D) of the equation is 0.
Discriminant of a quadratic equation ax² + bx + c = 0 is b² – 4ac
In the given equation, a = 1, b = 5k, and c = 16
b² – 4ac = 0
(5k)² – 4(1)(16) = 0
25k² – 64 = 0
k² = \\frac{64}{25})
k = ± \\frac{8}{5})

---

Question 3 Internal Choice 1: Write the value of cot²θ − \\frac{1}{sin^2θ})

Q3 Internal Choice 1 Video Explanation

Scroll down further for explanatory answer text

---

Explanatory Answer | Q3 Internal Choice 1

cot² θ − \\frac{1 }{sin^2 θ})
= \\frac{cos^2 θ}{sin^2 θ}) − \\frac{1}{sin^2 θ}) [Because cot θ = \\frac{cos θ}{sin θ})]
= \\frac{cos^2 θ − 1}{sin^2 θ})
= \\frac{− sin^2 θ}{sin^2 θ}) [Because sin² θ + cos² θ = 1 => sin² θ = 1 - cos² θ]
= -1

OR

Question 3 Internal Choice 2: If sin θ = cos θ, then find the value of 2tan θ + cos2 θ

Q3 Internal Choice 2 | Video Explanation

Scroll down further for explanatory answer text

---

Explanatory Answer | Q3 Internal Choice 1

For what values of θ will sin θ = cos θ?
sin θ = cos θ only when θ = 45°

Substitute θ = 45° in given expression
2tan θ + cos² θ = 2tan 45° + cos² 45°
= 2tan (1) + cos² (\\frac{1}{√2}))
= 2 + (\\frac{1}{2}))
= \\frac{5}{2})

---

Question 4: If nth term of an A.P. is (2n + 1), what is the sum of its first three terms?

Q4 Video Explanation

Scroll down further for explanatory answer text

---

Explanatory Answer | Q4 2019 Sample Question Paper

nth term of the given A.P. is (2n + 1)
Substitute n = 1 to find the first term of the A.P. a₁ = 2(1) + 1 = 3
Substitute n = 2 to find the second term of the A.P. a₂ = 2(2) + 1 = 5
Substitute n = 3 to find the third term of the A.P. a₃ = 2(3) + 1 = 7
Sum of the first three terms = 3 + 5 + 7 = 15

---

Question 5: In figure if AD = 6 cm, DB = 9 cm, AE = 8 cm and EC = 12 cm and ∠ADE = 48°. Find ∠ABC.

Q5 Video Explanation

Scroll down further for explanatory answer text

---

Explanatory Answer | Q5 2019 Sample Question Paper

Basic Proportionality Theorem: If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio.
AD = 6 cm, DB = 9 cm, AE = 8 cm and EC = 12 cm
\\frac{AD}{DB}) = \\frac{6}{9}) = \\frac{2}{3}); \\frac{AE}{EC}) = \\frac{8}{12}) = \\frac{2}{3})
\\frac{AD}{DB}) = \\frac{AE}{EC}) ∴ DE is parallel to BC
If DE is parallel to BC, corresponding angles will be equal.
∴ ∠ADE = ∠ABC = 48°

---

Question 6: After how many decimal places will the decimal expansion of \\frac{23}{2^4 × 5^3}) terminate?

Q6 Video Explanation

Scroll down further for explanatory answer text

---

Explanatory Answer | Q6 2019 Sample Question Paper

Any real number which has a decimal expansion that terminates can be expressed as a rational number whose denominator is a power of 10 i.e., power of 2 and 5.
Express the fraction in an equivalent form such that the powers of 2 and 5 of the denominator are equal. Ensures that the denominator is a power of 10.
\\frac{23}{2^4 × 5^3}) = \\frac{23}{2^4 × 5^3}) × \\frac{5}{5}) = \\frac{23 × 5}{2^4 × 5^4}) = \\frac{115}{10^4}) = 0.0115
The answer is 4 places.

---