Class 10 Maths Sample Question Paper | 2019

Section C contains 10 questions of 3 marks each. Scroll down for explanatory answer and video solution to all ten 3-mark questions.The questions appeared from the following topics: Real Numbers, Polynomials, Coordinate Geometry, Linear Equations, Quadratic Equations, Triangles, Circles, Trigonometric ratios, Surface Areas & Volumes, and Statistics.

13. Question 13

    Use Euclid's division algorithm to find the HCF of 726 and 275.

    Approach to Find HCF using Euclid's Division Lemma

    Step 1: Apply Euclid's Lemma to 726 with 275 as divisor.
    Step 2: If a remainder exists, apply the Lemma to the divisor of the preceding step (in this case 275) with remainder of the division of preceding step as the divisor.
    Step 3: Continue step 2 till the remainder obtained is 0.
    Step 4: The divisor of the last step is the HCF.
    

    Solution Video Solution Real Numbers

    ---

14. Question 14

    Find the zeroes of the following polynomial: 5√5 x² + 30x + 8√5

    Approach to solve this Polynomials problem

    Factorize the given quadratic polynomial by splitting the middle term.
    The product is 200 and the sum is 30. So, the middle term splits as 20x and 30x.

    Solution Video Solution Polynomials

    ---

15. Question 15

    Places A and B are 80 km apart from each other on a highway. A car starts from A and another from B at the same time. If they move in same direction they meet in 8 hours and if they move towards each other they meet in 1 hour 20 minutes. Find the speed of cars.

    Hint to solve this Linear Equations Word Problem

    Step 1: Let the speeds of cars A and B be x and y km/hr respectively.
    Step 2: When they travel for 8 hours, A will cover 8x km and B will cover 8y km.
    Step 3: Frame equation (1). When they travel in the same direction, the distance covered by A is 80 more than the distance covered by B. So, the difference in distance traveled (8x - 8y) is 80 km.
    Step 4: Frame equation (2) similarly when they travel in opposite direction.
    Step 5: Solve equations (1) and (2) to find the speeds of the cars.

    Solution Video Solution Linear Equations

    ---

16. Question 16 | Internal Choice A

    The points A(1, -2) , B(2, 3), C(k, 2) and D(-4, -3) are the vertices of a parallelogram. Find the value of k.

    Hint to solve this Coordinate Geometry problem

    Property: Diagonals of a parallelogram bisect each other. So, the coordinates of the mid points of the two diagonals are the same.
    Step 1: Using mid point formula compute mid points of AC and BD
    Step 2: Equate the two expressions to find k.
    

    Solution Video Solution Coordinate Geometry
    OR

    Question 16 | Internal Choice B

    Find the value of k for which the points (3k-1, k-2), (k, k-7) and (k-1, -k-2) are collinear.

    Approach to solve this Coordinate Geometry problem

    Step 1: Compute the area of the triangle with the above 3 points as the coordinates of the vertices.
    Step 2: Because the 3 points are collinear, the area of the triangle thus formed is 0.
    Step 3: Solve the equation to find k.
    

    Solution Video Solution Coordinate Geometry

    ---

17. Question 17 | Internal Choice A

    Prove that cot θ – tan θ = \\frac{\text{2 cos^2 θ – 1}}{\text{sin θ cos θ}})

    Hint to solve this Trigonometry problem

    Step 1: Express LHS in terms of sin θ and cos θ.
    Step 2: Take LCM of the resulting expression and apply trigonometric identity Sin² θ + Cos² θ = 1 in the numerator to arrive at the RHS.

    Solution Video Solution Trigonometry
    OR

    Question 17 | Internal Choice B

    Prove that sin θ(1 + tan θ) + cos θ(1 + cot θ) = sec θ + cosec θ

    Hint to solve this Trigonometry problem

    Step 1: Express tan θ and cot θ in the LHS in terms of sin θ and cos θ.
    Step 2: Simplify the expression to get RHS.

    Solution Video Solution Trigonometry

    ---

18. Question 18

    The radii of two concentric circles are 13 cm and 8 cm. AB is a diameter of the bigger circle and BD is a tangent to the smaller circle touching it at D and intersecting the larger circle at P on producing. Find the length of AP.

    Hint to solve this Circles problem

    Step 1: Establish similarity between Δ ABP and Δ OBD by AA similarity.
    Step 2: Therefore, AB/OB = AP/OD.
    Step 3: Substitute values of AB (diameter of larger circle), OB (radius of larger circle), and OD (radius of inner circle) to find AP
    

    Solution Video Solution Circles

    ---

19. Question 19 | Internal Choice A

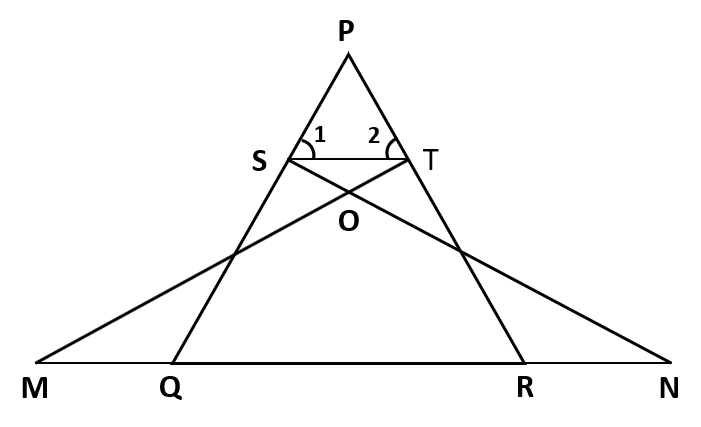
    In figure ∠1 = ∠2 and ΔNSQ =≈ Δ MTR, then prove that ΔPTS ~ ΔPRQ.

    Hint to solve this Triangles problem

    Step 1: Because ∠1 = ∠2, in Δ PTS, sides opposite to the angles PT and PS will be equal.
    Step 2: Because ΔNSQ ⩰ ΔMTR, by CPCT ∠NQS = ∠MRT.
    Step 3: But ∠NQS = ∠PQR and ∠MRT = ∠PRQ; so, ∠PQR = ∠PRQ.
    Step 4: ∴ in Δ PQR, sides opposite to the two angles will be equal. i.e., PR = PQ
    Step 5: Because PT = PS and PR = PQ, and ∠ P is common to both triangles Δ PTS and PQR, by SAS the two triangles are similar.
    

    Solution Video Solution Triangles
    OR

    Question 19 | Internal Choice B

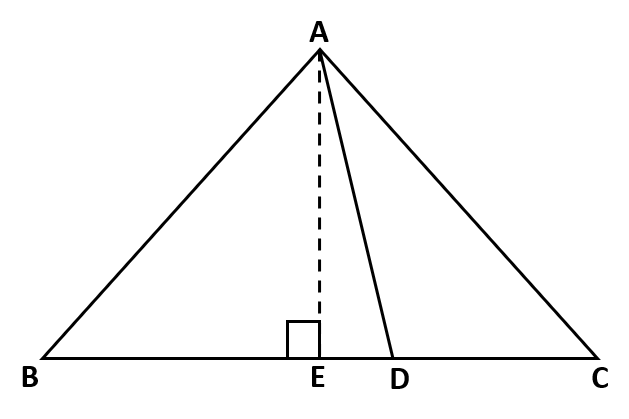
    In ΔABC, if AD is the median, then show that AB² + AC² = 2(AD² + BD²)

    Hint to solve this Triangles problem

    Step 1: Draw perpendicular AE to side BC from A.
    Step 2: Apply Pythagoras theorem on two right triangles AEB and AEC.
    Step 3: Add the two equations representing the two Pythagoras Theorem.
    Step 4: LHS of the addition is the LHS of what is to be proved. Rewrite AE, BE, and CE in terms of AD, ED, BD, ED, and CD, ED to get the RHS.
    

    Solution Video Solution Triangles

    ---

20. Question 20

    Find the area of the minor segment of a circle of radius 42 cm, if length of the corresponding arc is 44 cm.

    Hint to solve this Areas Related to Circles problem

    Step 1: Using length of arc and radius of circle, compute ∠AOB, the angle subtended by the sector at the center of the circle.
    Step 2: Compute area of sector OADB.
    Step 3: Compute area of equilateral triangle AOB.
    Step 4: Compute are of minor segment ADB.

    Solution Video Solution Areas Related to Circles

    ---

21. Question 21 | Internal Choice A

    Water is flowing at the rate of 15 km per hour through a pipe of diameter 14 cm into a rectangular tank which is 50 m long and 44 m wide. Find the time in which the level of water in the tank will rise by 21 cm.

    Hint to solve this Surface Areas and Volumes problem

    Step 1: Convert all units to metres for uniformity.
    Step 2: Compute volume of water flowing through the pipe in 1 hour using information about rate of flow of water through pipe and radius of pipe.
    Step 3: Compute volume of water added to the tank when its level rises by 21 cm.
    Step 4: Time taken = \\frac{\text{Volume of water added to taken}}{\text{volume flowing through pipe in 1 hour}})
    

    Solution Video Solution Surface Areas and Volumes
    OR

    Question 21 | Internal Choice B

    A solid sphere of radius 3 cm is melted and then recast into small spherical balls each of diameter 0.6 cm. Find the number of balls.

    Steps to solve this Surface Areas and Volumes problem

    Step 1: Number of balls = \\frac{\text{Volume of solid sphere}}{\text{Volume of 1 spherical ball}})
    Step 2: Compute volume of solid sphere. Radius = 3 cm.
    Step 3: Compute volume of each spherical ball. Raidus = 0.3 cm.
    Step 4: Substitute values from steps 2 and 3 in step 1 to find answer.
    

    Solution Video Solution Surface Areas and Volumes

    ---

22. Question 22

    The table shows the daily expenditure on grocery of 25 households in a locality. Find the modal daily expenditure on grocery by a suitable method.

    Daily Expenditure	100-150	150-200	200-250	250-300	300-350
    Frequency	4	5	12	2	2

    Steps to solve this Statistics Question

    Step 1: Identify modal class. Highest frequency is 12. So, modal class is 200 - 250.
    Step 2: Formula to compute Mode of grouped data = l + [ \\frac{f_1 – f_0}{2f_1 – f_0 − f_2}\\) ] × h
    Where l is the lower limit of the modal class & h is the size of the class, f₁ is the frequency of the modal class, f₀ is the frequency of the preceding class, f₂ is the frequency of the succeeding class.

    Solution Video Solution Statistics