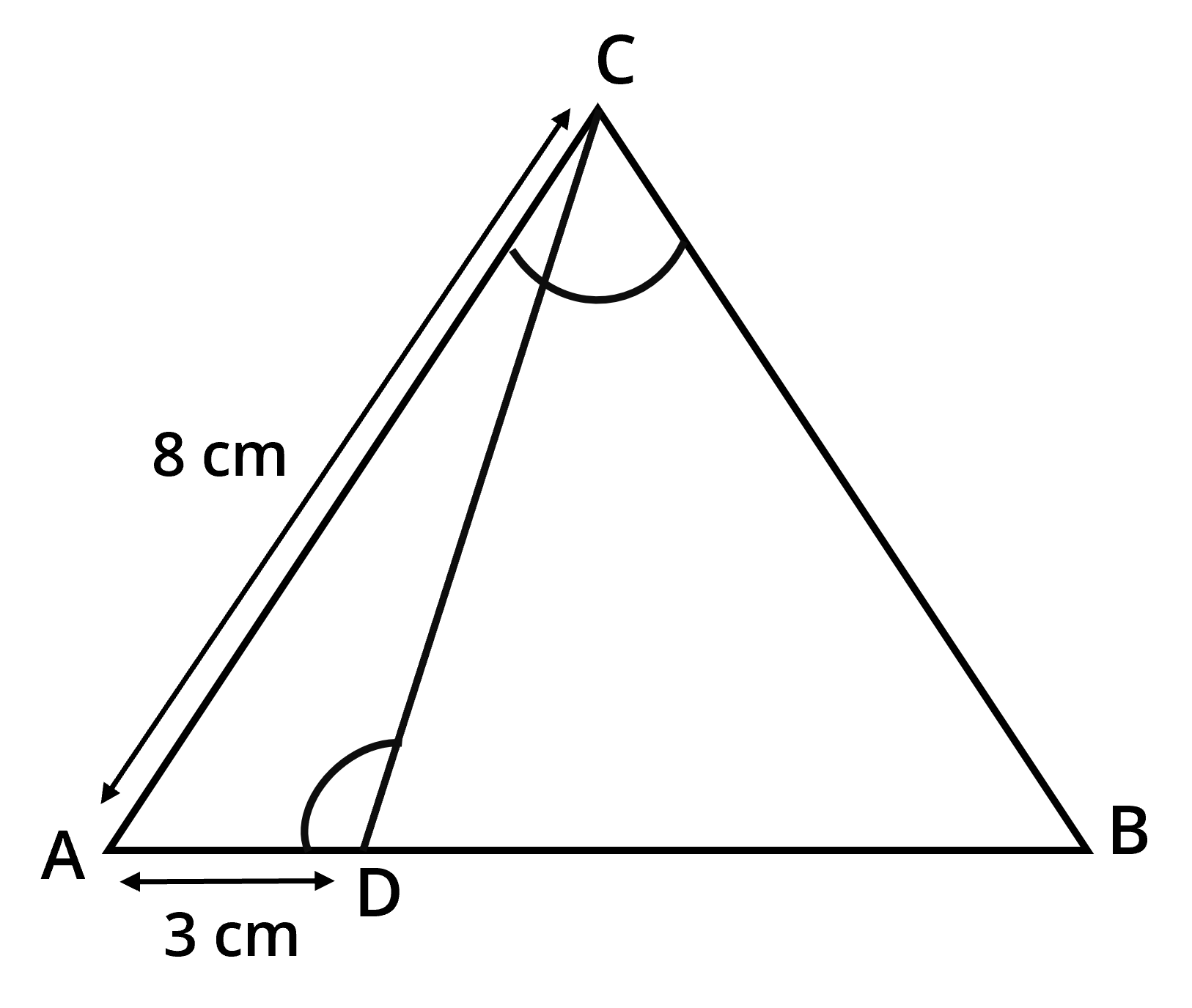Section B Solutions and Videos | 2021-22 Term I MCQ Sample Paper CBSE Class 10 Maths

Section B of the CBSE Class 10 Sample Paper (Standard) for Term I has 20 questions. All questions are multiple choice questions. All questions carry 1 mark each. You have to answer 16 out of the 20 questions. The following is the break up of the number of questions that appeared from each of the eight chapters that were part of the Term I syllabus.

Real Numbers 3 questions
A Pair of Linear Equations in 2 Variables 3 questions
Triangles 2 questions
Coordinate Geometry 3 questions
Introduction to Trigonometry 3 questions
Areas related to circles 3 question
Probability 2 questions
Polynomials 1 question

Section B 20 Multiple Choice Questions

Question 21

If sum of two numbers is 1215 and their HCF is 81, then the possible number of pairs of such numbers are
1. 2
2. 3
3. 4
4. 5
Choice C
Question 22

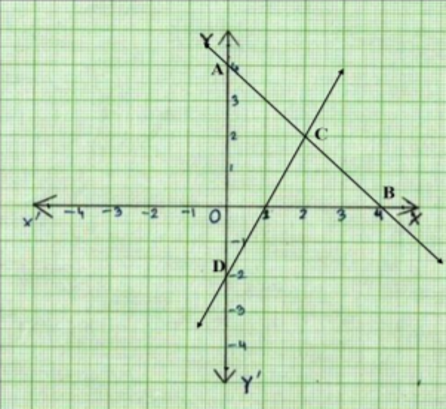
Given below is the graph representing two linear equations by lines AB and CD respectively. What is the area of the triangle formed by these two lines and the line x=0?
1. 3 sq.units
2. 4 sq.units
3. 6 sq.units
4. 8 sq.units
Choice C
Question 23

If tanα + cotα = 2, then tan²⁰α + cot²⁰α =
1. 0
2. 2
3. 20
4. 2²⁰
Choice B
Question 24

If 217x + 131y = 913, 131x + 217y = 827, then x + y is
1. 5
2. 6
3. 7
4. 8
Choice A
Question 25

The LCM of two prime numbers p and q (p > q) is 221. Find the value of 3p - q.
1. 4
2. 28
3. 38
4. 48
Choice C
Question 26

A card is drawn from a well shuffled deck of cards. What is the probability that the card drawn is neither a king nor a queen?
1. \\frac{11}{13})
2. \\frac{12}{13})
3. \\frac{11}{26})
4. \\frac{11}{52})
Choice A
Question 27

Two fair dice are rolled simultaneously. The probability that 5 will come up at least
1. \\frac{5}{36})
2. \\frac{11}{36})
3. \\frac{12}{36})
4. \\frac{23}{36})
Choice B
Question 28

If 1 + sin²α = 3sinαcosα, then values of cotα are
1. -1, 1
2. 0, 1
3. 1, 2
4. -1, -1
Choice C
Question 29

The vertices of a parallelogram in order are A(1, 2), B(4, y), C(x, 6) and D(3, 5). Then (x, y) is
1. (6, 3)
2. (3, 6)
3. (5, 6)
4. (1, 4)
Choice A
Question 30

In the given figure, ∠ACB = ∠CDA, AC = 8cm, AD = 3cm, then BD is
1. \\frac{22}{3})cm
2. \\frac{26}{3})cm
3. \\frac{55}{3})cm
4. \\frac{64}{3})cm
Choice
Question 31

The equation of the perpendicular bisector of line segment joining points A(4, 5) and B(-2, 3) is
1. 2x - y + 7 = 0
2. 3x + 2y - 7 = 0
3. 3x - y - 7 = 0
4. 3x + y - 7 = 0
Choice D
Question 32

In the given figure, D is the mid-point of BC, then the value of \\frac{cot x}{cot y})
1. 2
2. \\frac{1}{2})
3. \\frac{1}{3})
4. \\frac{1}{4})
Choice B
Question 33

The smallest number by which \\frac{1}{13}) should be multiplied so that its decimal expansion terminates after two decimal places is
1. \\frac{13}{100})
2. \\frac{13}{10})
3. \\frac{10}{13})
4. \\frac{100}{13})
Choice A
Question 34

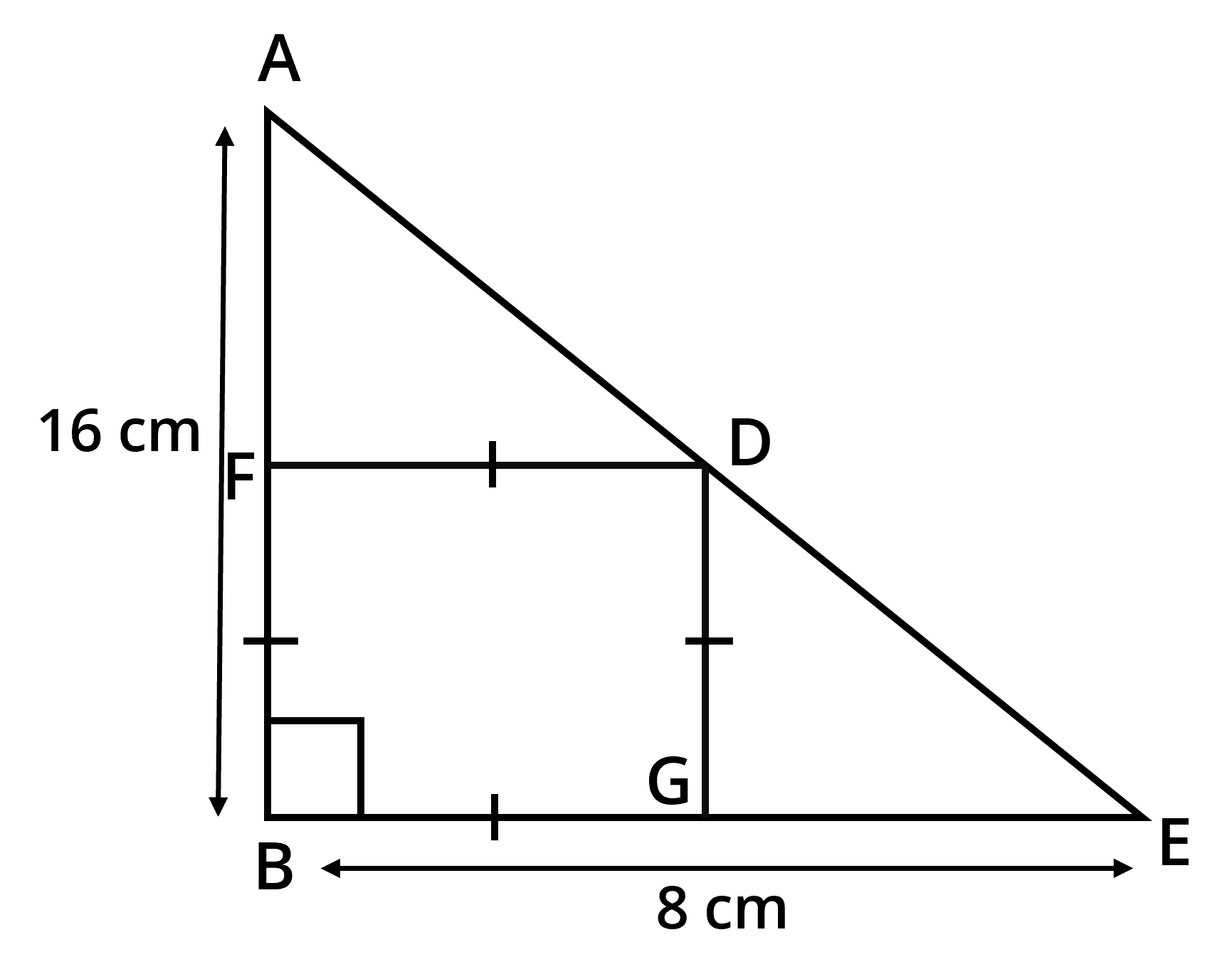
Sides AB and BE of a right triangle, right angled at B are of lengths 16 cm and 8 cm respectively. The length of the side of largest square FDGB that can be inscribed in the triangle ABE is
1. \\frac{32}{3})
2. \\frac{16}{3})
3. \\frac{8}{3})
4. \\frac{4}{3})
Choice
Question 35

Point P divides the line segment joining R(-1, 3) and S(9, 8) in ratio k : 1. If P lies on the line x - y + 2 = 0, then value of k is
1. \\frac{2}{3})
2. \\frac{1}{2})
3. \\frac{1}{3})
4. \\frac{1}{4})
Choice A
Question 36

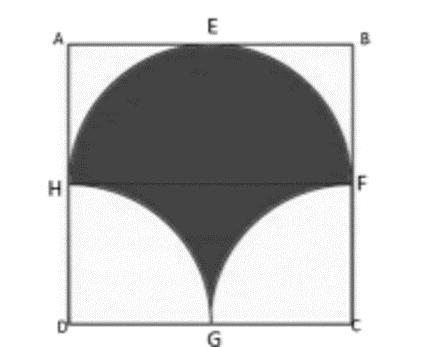
In the figure given below, ABCD is a square of side 14 cm with E, F, G and H as the mid points of sides AB, BC, CD and DA respectively. The area of the shaded portion is
1. 44 cm²
2. 49 cm²
3. 98 cm²
4. 49\\frac{\pi}{2}) cm²
Choice C
Question 37

Given below is the picture of the Olympic rings made by taking five congruent circles of radius 1cm each, intersecting in such a way that the chord formed by joining the point of intersection of two circles is also of length 1cm. Total area of all the dotted regions assuming the thickness of the rings to be negligible is
1. 4(\\frac{\pi}{12}) - \\frac{\sqrt{3}}{4}) ) cm²
2. (\\frac{\pi}{6}) - \\frac{\sqrt{3}}{4}) ) cm²
3. 4(\\frac{\pi}{6}) - \\frac{\sqrt{3}}{4}) ) cm²
4. 8(\\frac{\pi}{6}) - \\frac{\sqrt{3}}{4}) ) cm²
Choice D
Question 38

If 2 and \\frac{1}{2}) are the zeros of px² + 5x + r, then
1. p = r = 2
2. p = r = -2
3. p = 2, r = -2
4. p = -2, r = 2
Choice B
Question 39

The circumference of a circle is 100 cm. The side of a square inscribed in the circle is
1. 50\\sqrt{2}) cm
2. \\frac{100}{\pi}) cm
3. \\frac{50\sqrt{2}}{\pi}) cm
4. \\frac{100\sqrt{2}}{\pi}) cm
Choice C
Question 40

The number of solutions of 3^{x + y} = 243 and 243^{x - y} = 3 is
1. 0
2. 1
3. 2
4. infinite
Choice B