CBSE Sample Paper Solution | 2021-22 Section C

Section C of the CBSE Class 10 Sample Paper (Standard) for Term I has 10 questions. All questions are multiple choice questions. All questions carry 1 mark each. You have to answer 8 out of the 10 questions. The questions are based on two case studies, each comprising 5 questions.

Case Study 1: Questions 41 to 45

The figure given above shows the path of a diver, when she takes a jump from the diving board. Clearly it is a parabola. Annie was standing on a diving board, 48 feet above the water level. She took a dive into the pool. Her height (in feet) above the water level at any time 't' in seconds is given by the polynomial h(t) such that h(t) = -16t² + 8t + k.

41. Question 41

    What is the value of k?

    1. 0
    2. -48
    3. 48
    4. \\frac{48}{-16})

    Correct AnswerChoice C

    Video Solution Polynomials

    ---

42. Question 42

    At what time will she touch the water in the pool?

    1. 30 seconds
    2. 2 seconds
    3. 1.5 seconds
    4. 0.5 seconds

    Correct AnswerChoice B

    Video Solution Polynomials

    ---

43. Question 43

    Rita's height (in feet) above the water level is given by another polynomial p(t) with zeroes -1 and 2. Then p(t) is given by

    1. t² + t - 2
    2. t² + 2t - 1
    3. 24t² - 24t + 48
    4. -24t² + 24t + 48

    Correct AnswerChoice D

    Video Solution Polynomials

    ---

44. Question 44

    A polynomial q(t) with sum of zeroes as 1 and the product as -6 is modelling Anu's height in feet above the water at any time t( in seconds). Then q(t) is given by

    1. t² + t + 6
    2. t² + t - 6
    3. -8t² + 8t + 48
    4. 8t² - 8t + 48

    Correct AnswerChoice C

    Video Solution Polynomials

    ---

45. Question 45

    The zeroes of the polynomial r(t) = -12t² + (k-3)t + 48 are negative of each other. Then k is

    1. 3
    2. 0
    3. -1.5
    4. -3

    Correct AnswerChoice A

    Video Solution Polynomials

    ---

Case Study 2: Questions 46 to 50

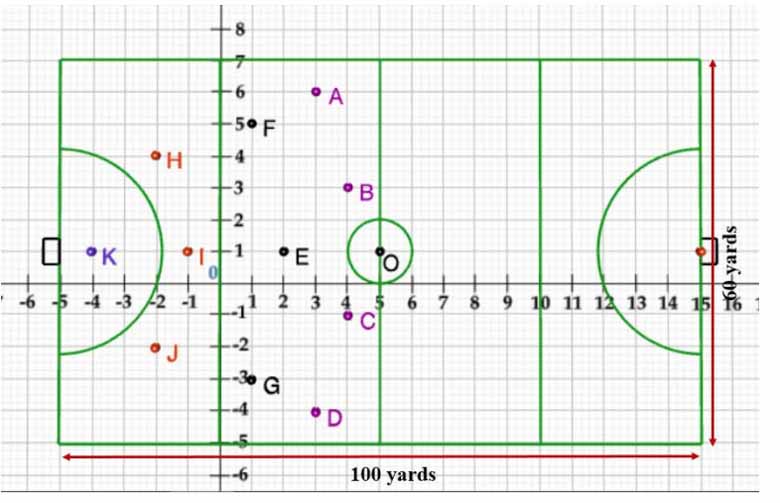
A hockey field is the playing surface for the game of hockey. Historically, the game was played on natural turf (grass) but nowadays it is predominantly played on an artificial turf. It is rectangular in shape - 100 yards by 60 yards. Goals consist of two upright posts placed equidistant from the centre of the backline, joined at the top by a horizontal crossbar. The inner edges of the posts must be 3.66 metres (4 yards) apart, and the lower edge of the crossbar must be 2.14 metres (7 feet) above the ground.

Each team plays with 11 players on the field during the game including the goalie. Positions you might play include-

• Forward: As shown by players A, B, C and D.
• Midfielders: As shown by players E, F and G.
• Fullbacks: As shown by players H, I and J.
• Goalie: As shown by player K

Using the picture of a hockey field below, answer the questions that follow

46. Question 46

    The coordinates of the centroid of ΔEHJ are

    1. (\\frac{-2}{3}), 1)
    2. (1, \\frac{-2}{3}))
    3. (\\frac{2}{3}), 1)
    4. (\\frac{-2}{3}), -1)

    Correct AnswerChoice A

    Video Solution Coordinate Geometry

    ---

47. Question 47

    If a player P needs to be at equal distances from A and G, such that A, P and G are in straight line, then position of P will be given by

    1. (\\frac{-3}{2}), 2)
    2. (2, \\frac{-3}{2}))
    3. (2, \\frac{3}{2}))
    4. (-2, -3)

    Correct AnswerChoice C

    Video Solution Coordinate Geometry

    ---

48. Question 48

    The point on x axis equidistant from I and E is

    1. (\\frac{1}{2}), 0)
    2. (0, \\frac{-1}{2}))
    3. (\\frac{-1}{2}), 0)
    4. (0, \\frac{1}{2}))

    Correct AnswerChoice A

    Video Solution Coordinate Geometry

    ---

49. Question 49

    What are the coordinates of the position of a player Q such that his distance from K is twice his distance from E and K, Q and E are collinear?

    1. (1, 0)
    2. (0, 1)
    3. (-2, 1)
    4. (-1, 0)

    Correct AnswerChoice B

    Video Solution Coordinate Geometry

    ---

50. Question 50

    The point on y axis equidistant from B and C is

    1. (-1, 0)
    2. (0, -1)
    3. (1, 0)
    4. (0, 1)

    Correct AnswerChoice D

    Video Solution Coordinate Geometry

    ---