Extra Questions For Class 10 Maths Chapter 8 | Q1

This CBSE class 10 Maths practice question is from the topic Trigonometry. It tests your understanding of the concepts of trigonometric ratios of a right triangle and application of Pythagoras Theorem. This extra question also helps you remember a popular Pythagorean Triplet.

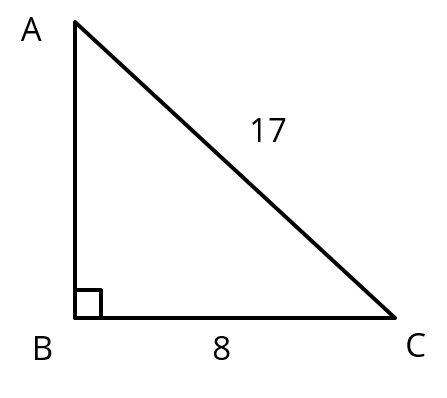
Question 1 : Consider right triangle ABC, right angled at B. If AC = 17 units and BC = 8 units determine all the trigonometric ratios of angle C.

---

Video Explanation

---

---

Explanatory Answer | Trigonometry Important Questions Q1

Given Data

Length of the side BC = 8 units
Length of the side AC = 17 units

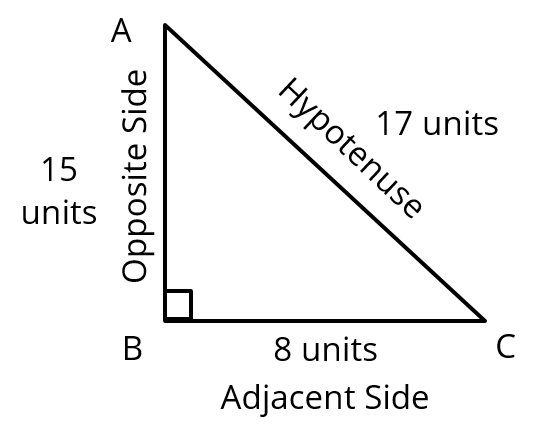
Step 1: Calculate the length of AB

In Δ ABC, using Pythagoras theorem, AB = \\sqrt{AC^2− BC^2 })= \\sqrt{17^2− 8^2})
\\sqrt{289−64}) = \\sqrt{225})
⇒ AB = 15 units

Step 2: Calculate the trigonometric ratios of angle C

sin C = \\frac{\text{opposite side}}{\text{hypotenuse}})=\\frac{\text{AB}}{\text{AC}})= \\frac{15}{17})
cos C = \\frac{\text{adjcent side}}{\text{hypotenuse}})=\\frac{\text{BC}}{\text{AC}})= \\frac{8}{17})
tan C =\\frac{\text{opposite side}}{\text{adjcent side}}) =\\frac{\text{AB}}{\text{BC}})= \\frac{15}{8})
cot C =\\frac{\text{1}}{\text{tan ⁡C}}) =\\frac{\text{adjcent side}}{\text{opposite side}}) = \\frac{\text{BC}}{\text{AB}}) = \\frac{8}{15})
sec C = \\frac{\text{1}}{\text{cos ⁡C}}) = \\frac{\text{hypotenuse}}{\text{adjcent side}}) = \\frac{\text{AC}}{\text{BC}})= \\frac{17}{8})
cosec C = \\frac{\text{1}}{\text{sin ⁡C}}) = \\frac{\text{hypotenuse}}{\text{opposite side}}) =\\frac{\text{AC}}{\text{AB}})= \\frac{17}{15})