Trigonometry Extra Questions | Class 10 Maths | Q3

This CBSE class 10 Maths additional practice question is from the topic Trigonometry. Concepts Covered: Trigonometric Values, Pythagoras Theorem, and Similarity of Triangles.

Question 3 : If C and Z are acute angles and that cos C = cos Z prove that ∠C = ∠Z .

Video Explanation

Explanatory Answer | Trigonometry Important Question 3

Let us assume two right triangles ΔABC and ΔXYZ

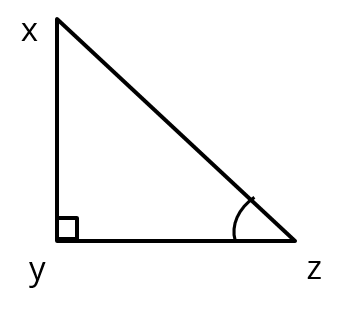
Given C and Z are acute angles and cos C = cos Z
cos C = \\frac{\text{BC}}{\text{AC}}) and cos Z = \\frac{\text{YZ}}{\text{XZ}})
cos C = cos Z =>\\frac{\text{BC}}{\text{AC}})= \\frac{\text{YZ}}{\text{XZ}})
Let \\frac{\text{BC}}{\text{YZ}})= \\frac{\text{AC}}{\text{XZ}}) = k..... (1)
BC = k(yz) and AC = k(xz)

In right triangle ABC, using Pythagoras theorem AB = \\sqrt{AC^2− BC^2 })
AB = \\sqrt{(k(xz)^2−(k(yz)^2)})= k\\sqrt{(xz)^2− (yz)^2 })
In right triangle xyz, using Pythagoras theorem xy = \\sqrt{(xz)^2− (yz)^2 })
\\frac{\text{AB}}{\text{XY}}) = \\frac{K × \sqrt{(X Z)^{2}-(Y Z)^{2}}}{\sqrt{(X Z)^{2}-(Y Z)^{2}}})
Or \\frac{\text{AB}}{\text{XY}}) = k ..... (1)

From 1 and 2, \\frac{\text{BC}}{\text{YZ}}) = \\frac{\text{AC}}{\text{XZ}}) = \\frac{\text{AB}}{\text{XY}}) = k
By SSS similarity criterion, we can conclude ΔABC is similar to ΔXYZ
∴ Corresponding angles of two similar triangles will be equal.
∴ ∠C = ∠Z