Extra Questions For Class 10 Maths Chapter 8 #4

This CBSE class 10 Maths practice question is from the topic Trigonometry. It tests the concept of trigonometric values of complementary angles.

Question 4 : In ΔABC right angled at B, sin C = \\frac{\text{5}}{\text{13}}). Find
(i) sin A
(ii) cos A
(iii) cos C

---

Video Explanation

---

---

Explanatory Answer | Trigonometry Extra Question 4

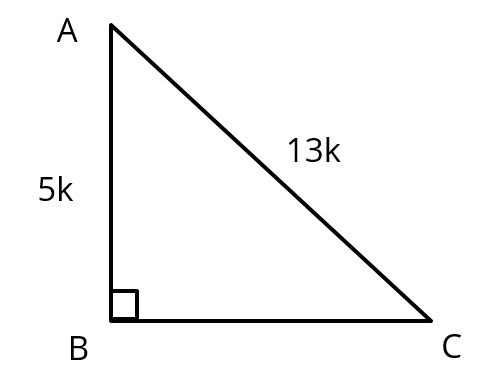
sin C = \\frac{\text{side opposite to ∠C}}{\text{hypotenuse}})=\\frac{\text{AB}}{\text{AC}})= \\frac{\text{5}}{\text{13}}) ...... (1)
Let AB = 5k and AC = 13k

Calculate Sine and Cosine values of the angles

Using Pythagoras theorem, BC = \\sqrt{AC^2− AB^2});
BC = \\sqrt{(13k)^2− (5k)^2 }) = \\sqrt{169 k^2− 25 k^2 }) = \\sqrt{144k^2 }) = 12k

sin A = \\frac{\text{side opposite to ∠A}}{\text{hypotenuse}})= \\frac{\text{BC}}{\text{AC}})= \\frac{\text{12k}}{\text{13k}})= \\frac{\text{12}}{\text{13}}) ...... (2)

cos A = \\frac{\text{side adjcent to ∠ A}}{\text{hypotenuse}}) = \\frac{\text{AB}}{\text{AC}})= \\frac{\text{5k}}{\text{13k}})= \\frac{\text{5}}{\text{13}}) ...... (3)

cos C = \\frac{\text{side adjcent to ∠ C}}{\text{hypotenuse}})= \\frac{\text{BC}}{\text{AC}}) = \\frac{\text{12k}}{\text{13k}}) = \\frac{\text{12}}{\text{13}}) ...... (4)

Inference
From (1) and (3): sin A = cos C
From (2) and (4): sin C = cos A

Why?

If ABC is right angled at B, side adjacent to ∠ A will be the side opposite to ∠C.
Similarly side opposite to ∠A will be the side adjacent to ∠C.
i.e., ∠A = 90° - ∠C and ∠C = 90° - ∠A