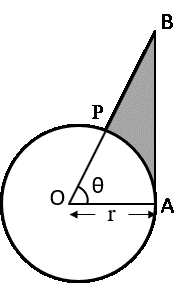
Question: In figure given below, is shown a sector OAP of a circle with centre O, containing ∠θ. AB perpendicular to the radius OA and meets OP produced at B. Prove that the perimeter of shaded region is r[tan θ + secθ + \\frac{πθ}{180-1})
Video Explanation
Explanatory Answer

Step 1: Find AB
In right triangle OAB, tanθ = \\frac{AB}{OA}) = \\frac {AB}{r})
∴ AB = r tanθ
Step 2: Find PB
PB = OB – OP
In right triangle OAB, secθ = \\frac{OB}{OA}) = \\frac{OB}{r})
∴ OB = r secθ
OP = r
Hence, PB = r secθ – r
Step 3: Length of arc AP = \\frac{θ}{360}) × 2πr = \\frac{πθ}{180}) × r
Perimeter of shaded region = AB + PB + arc AP
= r tanθ + r secθ – r + \\frac{πθ}{180}) × r
= r (tanθ + secθ – 1 + \\frac{πθ}{180}))