Class 10 2016 Maths | CBSE Previous Year Paper Solutions | Section B 2 mark questions video solutions

Section B contains 6 questions of 2 marks each. Scroll down for explanatory answer and video solution to all six 2-mark questions that appeared in 2016 CBSE Class 10 Board Exam maths paper. The questions appeared from the following topics: Quadratic Equations, Coordinate Geometry, Circles, and Arithmetic Progressions.

If -5 is a root of the quadratic equation 2x² + Px – 15 = 0 and the quadratic equation P(x² + x) + K = 0 has equal roots, find the value of K.

Hint to solve this quadratic equations question

Step 1: Substitute x = -5 in the first quadratic equation and compute the value of P.
Step 2: Substitute the value of P computed in step 1 in the 2nd quadratic equation.
Step 3: Compute discriminant of second quadratic equation and equate it to zero to find the value of K.
Let P and Q be the points of trisection of the line segment joining the points A(2, –2) and B(–7, 4) such that P is nearer to A. Find the coordinates of P and Q.

Hint to solve this Coordinate Geometry problem

A medium difficulty 2 mark question that appeared in CBSE class 10 maths paper 2016.

Concept: Application of section formula
Approach: Step 1: Line segment AB is divided into 3 parts. AP, PQ, QB.
Step 2: Point P divides AB in the ratio 1 : 2. Apply section formula and compute coordinates of point P.
Step 3: Point Q divides AB in the ratio 2 : 1. Apply section formula and compute coordinates of point Q.
A quadrilateral ABCD is drawn to circumscribe a circle, with centre O, in such a way that the sides AB, BC, CD and DA touch the circle at the points P, Q, R and S respectively. Prove that AB +CD = BC + DA.

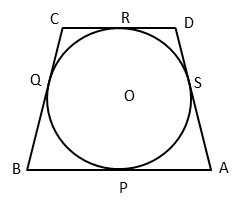
Hint to solve this Circles problem

Concept: From an external point, two tangents can be drawn to a circle. Both tangents are equal in length.
Approach: Assign variables for tangents from the 4 vertices. Let's say t1, t2, t3, and t4. Express AB, CD, BC, and AD in terms of t1, t2, t3, and t4 and prove the equation.
Prove that the points (3, 0), (6, 4) and (–1, 3) are the vertices of a right angled isosceles triangle.

Hint to solve this Coordinate Geometry problem

Approach: Solving this question requires usage of distance formula. Distance between two points (x₁, y₁) and (x₂, y₂) = \\sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2})
Step 1: Compute the lengths of the 3 sides of the triangle.
Step 2: Establish that the 3 sides of the triangle satisfy Pythagoras Theorem and that two sides of the triangle are equal.
The 4th term of an A.P. is zero. Prove that the 25th term of the A.P. is three times its 11th term.

Hint to solve this Arithmetic Progressions problem

Approach: n^th term of an Arithmetic Progression a_n = a₁ + (n - 1)d, where d is the common difference and a₁ is the first term of the A.P.
Step 1: Express a₄ using the above mentioned formula and equate it to zero. From this equation, we will get a relation between a₁ and d.
Step 2: a₁₁ using the above formula. Substitute a₁ in terms of d and express a₁₁ only in terms of a₁.
Step 3: a₂₅ using the above formula. Substitute a₁ in terms of d and express a₂₅ only in terms of a₁.
Step 4: Both a₁₁ and a₂₅ are now in terms of a₁. Prove the relation asked in the question.
From an external point P, two tangents PT and PS are drawn to a circle with centre O and radius r. If OP = 2r, show that ∠OTS = ∠OST = 30°.

Hint to solve this Circles problem

Concept: Knowledge of Sine of angles. Right triangle properties.
Step 1: Two congruent right triangles are formed between the two tangents and OP, where OP is the hypotenuse and one of the perpendicular sides of the two triangles is the radius of the circle.
Step 2: Because OP = 2r, using Sin ∠OPT, we can deduce ∠OPT = 30°
Step 3: Therefore, ∠POT = ∠QOT = 60°
Step 4: Triangle OST is isosceles. So, ∠OTS = ∠OST = 30°