2016 CBSE Class 10 Maths Board Paper | 4 Mark Question Solution & Videos

Section D contains 11 questions of 4 marks each. Scroll down for explanatory answer and video solution to the 4-mark questions that appeared in Class 10 Maths CBSE board exam in 2016. Questions appeared from the following chapters : Surface Areas & Volumes, Circles, Quadratic Equations, Applications of Trigonometry, Arithmetic Progressions, Coordinate Geometry, and Probability.

Due to heavy floods in a state, thousand were rendered homeless. 50 schools collectively offered to the state government to provide place and the canvas for 1500 tents to be fixed by the government and decided to share the whole expenditure equally. The lower part of each tent is cylindrical of base radius 2.8 m and height 3.5 m, with conical upper part of same base radius but of height 2.1 m. If the canvas used to make the tents costs 120 per sq.m, find the amount shared by each school to set up the tents. What value is generated by the above problem? (use = π \\frac{22}{7}))

How to solve this Surface Areas & Volume problem?

Step 1: Area of canvas for each tent = Curved surface area of cylindrical base + Curved surface area of cone.
Step 2: Number of tents sponsored by each school = 1500 / 50 = 30
Step 3: Area of canvas sponsored by each school = 30 × area of canvas for each tent.
Step 4: Cost shared by each school = Area of canvas shared by each school × per sq m cost of canvas.
Prove that the lengths of two tangents drawn from an external point to a circle are equal.

The same question appeared in 2017 board paper.

How to solve this Circles question?

Step 1: The tangent, radius, and the line joining the centre of the circle to point from where the tangent is drawn form a right triangle.
Note: Because two tangents can be drawn from the external point, we have two right triangles.
Step 2: Compute lengths of the two tangents using Pythagoras Theorem.
Step 3: The two right triangles have a common hypotenuse and one of their perpendicular sides is the radius of the circle. Hence, the tangents will measure the same.

In the figure given below, two equal circles, with centres O and O’, touch each other at X. OO’ produced meets the circle with centre O’ at A. AC is tangent to the circle with O, at the point C. O’D is perpendicular to AC. Find the value of \\frac{DO'}{CO})

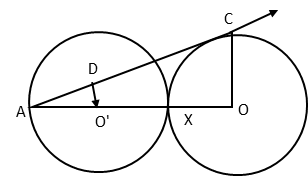
Hint to solve this Circles problem

Step 1: ▵ AO'D and ▵ AOC are similar by AA test.
Step 2: AO'/AO = DO'/CO
Step 3: AO' = r; AO = AX + XO = 2r + r = 3r
Solve for x: \\frac{1}{x + 1}) + \\frac{2}{x + 2}) = \\frac{4}{x + 4}), x ≠-1,-2,-4.

Hint to solve this Quadratic Equations problem

Step 1: Take (x + 1)(x + 2) as the common denominator for the LHS.
Step 2: Cross multiply and simplify the equation to get a quadratic equation.
Step 3: Use the quadratic formula to find the value of x.
The angle of elevation of the top Q of a vertical tower PQ from a point x on the ground is 60⁰. From a point y, 40 m vertically above x, the angle of elevation of the top Q of tower is 45⁰. Find the height of the tower PQ and the distance PX. (Use \\sqrt3) = 1.73).

Hint to solve this Applications of trigonometry problem

Step 1: Angle of elevation from point Y is 45°. Apply tan 45 in right triangle QZY. Let ZY = QZ = d.
Step 2: Angle of elevation from point X is 60°. Apply tan 60 in right triangle QPX. An expression in d.
Step 3: Solve for 'd' and find the answer.
The houses in a row are numbered consecutively from 1 to 49. Show that there exists a value of x such that sum of numbers of houses proceeding the house numbered x is equal to sum of the numbers of houses following x.

Hint to solve this Arithmetic Progressions problem

Condition: Sum of house numbers from 1 to (x − 1) = Sum of house numbers from (x + 1) to 49.
Step 1: Use AP summation formula to compute both LHS and RHS and solve for x to arrive at the answer.
In the figure below, the vertices of ∆ ABC are A (4, 6), B(1, 5) and C (7, 2). A line -segment DE is drawn to intersect the sides AB and AC at D and E respectively such that \\frac{AD}{AB}) = \\frac{AE}{AC}) = \\frac{1}{3}) calculate the area of ∆ ADE and compare it with area of ∆ABC.

Hint to solve this Coordinate Geometry problem

Step 1: AD : DB = AE : EC = 1 : 2
Step 2: Using section formula compute coordinates of D and E.
Step 3: Calculate area of triangle ABC using the coordinates of points A, B, and C.
Step 4: Calculate area of triangle ADE using the coordinates of points A, D, and E.
Step 5: Compute the ratio of the areas.
A number x is selected at a random from the numbers 1, 2, 3 and 4. Another number y is selected at random from the numbers 1, 4, 9 and 16. Find the probability that product of x and y is less than 16.

Hint to solve this Probability problem

Step 1: The product xy will take a total of 16 values. List down all 16 values. 16 is the denominator to be used when computing the probability.
Step 2: Count from the list the values that are less than 16. This count is the numerator to be used when computing the probability.
In figure given below, is shown a sector OAP of a circle with centre O, containing ∠θ. AB perpendicular to the radius OA and meets OP produced at B. Prove that the perimeter of shaded region is r[tanθ + sec⁡θ + \\frac{πθ}{180-1}])

Hint to solve this Circles problem

Step 1: Compute AB in terms of 'r' and θ in right triangle OAP. AB = r tanθ
Step 2: Compute PB = OB - OP. OB = r secθ
Step 3: Compute length of arc AP
Step 4: Sum of expressions obtained in steps 1 to 3 is the answer to the question.
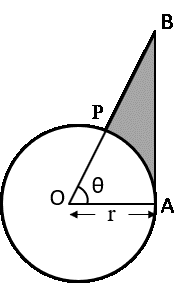
A motor boat whose speed is 24 km/h in still water takes 1 hour more to go 32 km upstream than to return downstream to the same spot. Find the speed of the stream.

Hint to solve this Quadratic Equations problem

Step 1: Assign a variable for the speed of the stream. Let it be x km/hr
Step 2: Compute time taken to travel 32 km upstream.
Step 3: Compute time taken to travel 32 km downstream.
Step 4: Time taken to travel 32 km upstream = time taken to travel 32 km downstream + 1 hour
Step 5: Solve the above equation for x.