CBSE Class 10 Maths Question Paper 2016 | Three mark question Solution & Videos

Section C contains 10 questions of 3 marks each. Scroll down for explanatory answer and video solution to all ten 3-mark questions that appeared in Class 10 Maths CBSE board exam in 2016. Questions appeared from the following chapters : Areas Related to Circles, Surface Areas & Volumes, Coordinate Geometry, Arithmetic Progressions, Quadratic Equations, Applications of Trigonometry, and Probability.

O is the centre of a circle such that diameter AB = 13 cm and AC = 12 cm. BC is joined. Find the area of the shaded region. (Take π = 3.14)

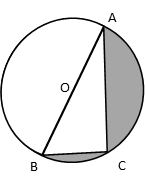
Hint to solve this Areas Related to Circles Question

Step 1: Because AB is a diameter, ▵ ACB is a right triangle.
Step 2: Using Pythagoras Theorem compute length of BC.
Step 3: Area of shaded region = Area of semicircle whose diameter is 13 - area of right triangle ACB.
A tent is in the shape of a cylinder surmounted by a conical top of same diameter. If the height and diameter of cylindrical part are 2.1 m and 3 m respectively and the slant height of conical part is 2.8 m, find the cost of canvas needed to make the tent if the canvas is available at the rate of ` 500/sq.metre. (Use π = \\frac{22}{7}))

Hint to solve this Surface Areas & Volumes problem

Step 1: Cost of canvas = Area of canvas × Cost per sqm.
Step 2: Area of canvas = CSA of cylinder + CSA of cone
If the point P(x, y) is equidistant from the points A(a + b, b – a) and P(a – b, a + b). Prove that bx = ay.

Hint to solve this Coordinate Geometry problem

Concept: Distance Formula

Step 1: Compute the length of the line segment PA using the distance formula.
Step 2: Compute the length of the line segment PB using the distance formula.
Step 3: Because P is equidistant from A and B, equate PA and PB. Essentially, equate PA² and PB².
Find the area of the shaded region, enclosed between two concentric circles of radii 7 cm and 14 cm where ∠AOC = 40°. (Use π = \\frac{22}{7}).)

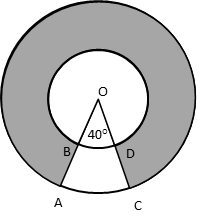
Hint to solve this Areas Related to Circles problem

Step 1: The shaded region is a circular disc that subtends an angle of 320° at the centre of the circle.
Step 2: Area of circular disc = Area of outer circle - Area of inner circle.
Step 3: 320/360 × area of circular disc is the area of the shaded region.
If the ratio of the sum of first n terms of two A.P's is (7n + 1) : (4n + 27), find the ratio of their m^th terms.

Hint to solve this Arithmetic Progressions problem

Step 1: Write the sum of the n^th term of the two APs and equate the ratio to the ratio given in the question.
Step 2: Express ratio of the mth term of the two APs.
Step 3: Compare the two ratios and express n in terms of m. Substitute 'n' in terms of m in the first ratio to arrive at the answer.
Solve for x : \\frac{1}{(x-1)(x-2)}) + \\frac{1}{(x-2)(x-3)}) = \\frac{2}{3}). x ≠ 1, 2, 3.

Hint to solve this Quadratic Equations problem

Step 1: Take (x - 1)(x - 2)(x - 3) as common denominator of the LHS of the expression and simplify the numerator of the resultant expression.
Step 2: Cross multiply and simplify terms to get a quadratic equation.
Step 3: Solve the quadratic equation to compute the value of x.
A conical vessel, with base radius 5 cm and height 24 cm, is full of water. This water is emptied into a cylindrical vessel of base radius 10 cm. Find the height to which the water will rise in the cylindrical vessel, (Use π = \\frac{22}{7}))

Hint to solve this Surface Areas & Volume problem

Concept: Volume of water in the conical vessel = Volume of water emptied into the cylindrical vessel.
Step 1: Assign variable 'h' for the increase in height of water in the cylindrical vessel and solve for h.
A sphere of diameter 12 cm, is dropped in a right circular cylindrical vessel, partly filled with water. If the sphere is completely submerged in water, the water level in the cylindrical vessel rises by 3\\frac{5}{9}) cm. Find the diameter of the cylindrical vessel.

Hint to solve this Surface Areas & Volumes problem

Concept: Volume of sphere dropped = Volume of water displaced in cylindrical vessel.
Step 1: Assign variable 'r' for the radius of the cylindrical vessel.
Step 2: Equate the two volumes. One equation, one variable. Solve for 'r' to arrive at the answer.
A man standing on the deck of a ship, which is 10 m above water level, observes the angle of elevation of the top of a hill as 60° and the angle of depression of the base of hill as 30°. Find the distance of the hill from the ship and the height of the hill.

Hint to solve this Applications of Trigonometry problem

Step 1: Applying trigonometric ratio tan the angle of depression, compute the distance between the ship and the hill
Step 2: Applying tan of the angle of elevation, compute the height of the portion of the hill above the deck of the ship.
Step 3: Finally compute height of hill.
Three different coins are tossed together. Find the probability of getting
(i) exactly two heads
(ii) at least two heads
(iii) at least two tails.

Hint to solve this Probability problem

Step 1: The denominator for all 3 parts is the same = 8 outcomes.
Step 2: Compute the number of outcomes in which exactly two heads appear to find the answer for part i.
Step 3: Part ii) What does at least 2 heads mean? 2 or 3 heads.
Step 4: Part iii) What does at least 2 tails mean? 2 or 3 tails.