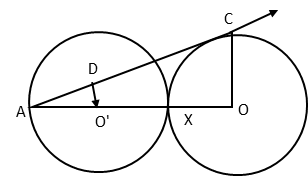
Question In the figure given below, two equal circles, with centres O and O’, touch each other at X. OO’ produced meets the circle with centre O’ at A. AC is tangent to the circle with O, at the point C. O’D is perpendicular to AC. Find the value of \\frac{DO'}{CO})
Video Explanation
Explanatory Answer

Both circles have the same radii.
OC is perpendicular to AC because a tangent and radius will be at right angles at the point where the tangent meets the circle.
From question, we know that O'D is perpendicular to AC.
By AA test of similarity, triangles AO'D and AOC are similar. (∠A is common to both triangles. ∠D and ∠C are 900.)
∴ the ratio of the corresponding sides will be the same.
\\frac{AO'}{AO}) = \\frac{DO'}{CO})
AO' = Radius of circle = r
AO = AX + XO = 2r + r =3r (AX is diameter of the circle with center O'. ∴ AX = 2r)
\\frac{AO'}{AO}) = \\frac{1}{3}) = \\frac{DO'}{CO})
