Question Prove that the lengths of two tangents drawn from an external point to a circle are equal.
Video Explanation
Explanatory Answer
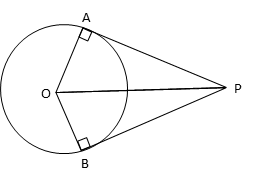
PA and PB are tangents drawn to circle with center ‘O’ from external point P.
The angle between the radius and the tangents where the tangents meet the circle is a right angle.
So, ∠OAP = ∠OBP = 90°
OP is a common hypotenuse of right triangles OAP and OBP.
OB and OA are radii to the circle and are equal.
In right ΔOAP, PA = \\sqrt {{OP}^{2}-{OA}^{2}})
In right ΔOBP, PB = \\sqrt {{OP}^{2}-{OB}^{2}})
Because OA = OB, \\sqrt {{OP}^{2}-{OA}^{2}}) = \\sqrt {{OP}^{2}-{OB}^{2}})
Or PA = PB
