If the points A(k + 1, 2k), B(3k, 2k + 3) and C(5k – 1, 5k) are collinear, then find the value of k.
Construct a triangle ABC with side BC = 7 cm, ∠B = 45o, ∠A = 105o. Then construct another triangle whose sides are \\frac{3}{4}) times the corresponding sides of the △ABC.
Two different dice are thrown together. Find the probability that the numbers obtained have
(i) even sum, and
(ii) even product
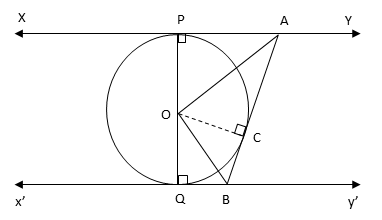
In the given figure, XY and X’Y’ are two parallel tangents to a circle with centre O and another tangents AB with point of contact C, is intersecting XY at A and X’Y’ at B. Prove that ∠AOB = 90o.
In a rain–water harvesting system, the rain-water from a roof of 22 m × 20 m drains into a cylindrical tank having diameter of base 2 m and height 3.5 m. If the tank is full, find the rainfall in cm. Write your views on water conservation.
Prove that the lengths of two tangents drawn from an external point to a circle are equal.
If the ratio of the sum of the first n terms of two A.Ps is (7n + 1) : (4n + 27), then find the ratio of their 9th terms.
Solve for x: \\frac{x - 1}{2x + 1} + \frac{2x + 1}{x - 1} = 2), where ≠ \\frac{-1}{2}), 1
A takes 6 days less than B to do a work. If both A and B working together can do it in 4 days, how many days will B take to finish it?
From the top of a tower, 100 m high, a man observe two cars on the opposite sides of the tower and in same straight line with its base, with its base, with angles of depression 30o and 45o. Find the distance between the cars. Take √3 = 1.732
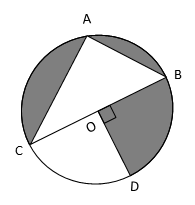
In the given figure, O is centre of the circle with AC = 24 cm, AB = 7 cm and ∠BOD = 90o. Find the area of the shaded region.