Question From the top of a tower, 100 m high, a man observes two cars on the opposite sides of the tower and in same straight line with its base, with angles of depression 30° and 45°. Find the distance between the cars. [Take \\sqrt {3}) = 1.732]
Video Explanation
Explanatory Answer
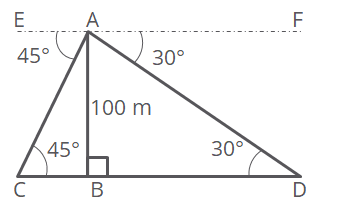
Let AB be the tower of height 100 m.
Let ‘C’ be the point where one of the cars is observed and ‘D’ be the point where the second car is observed.
∠EAC = 45°. Therefore, ∠BCA = 45°
Angle of depression = angle of elevation
Similarly, ∠FAD = ∠BDA = 30°
In right triangle ABC, tan 45° = \\frac{AB}{BC})
tan 45° = 1. Therefore, \\frac{AB}{BC}) = 1
or AB = BC = 100m
In right triangle ABD, tan 30° = \\frac{AB}{BD})
tan 30° = \\frac{1}{\sqrt {3}}). Therefore, \\frac{1}{\sqrt {3}}) = \\frac{100}{BD})
or BD = 100\\sqrt {3})
Take \\sqrt {3}) = 1.732
Therefore, BD = 100(1.732) = 173.2
Distance between the cars = CB + BD
= 100 + 173.2
= 273.2 m
