On a straight line passing through the foot of a tower, two points C and D are at distances of 4 m and 16 m from the foot respectively. If the angles of elevation from C and D of the top of the tower are complementary, then find the height of the tower.
A bag contains 15 white and some black balls. If the probability of drawing a black ball from the bag is thrice that of drawing a white ball, find the number of black balls in the bag.
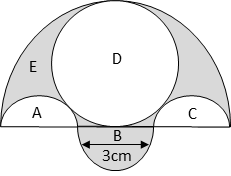
Three semicircles each of diameter 3 cm, a circle of diameter 4.5 cm and a semicircle of radius 4.5 cm are drawn in the given figure. Find the area of the shaded region.
In what ratio does the point \{({\frac{24}{11}, 1})}) divide the line segment joining the points P(2, -2) and Q(3, 7)? Also find the value of y.
Water in a canal, 5.4 m wide and 1.8 m deep, is flowing with a speed of 25 km/hour. How much area can it irrigate in 40 minutes, if 10 cm of standing water is required for irrigation?
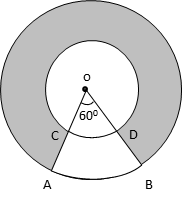
In the given figure, two concentric circles with centre O have radii 21 cm and 42 cm. If ∠AOB = 60o, find the area of the shaded region. Use π = \\frac{22}{7})
The dimensions of a solid iron cuboid are 4.4 m × 2.6 m × 1.0 m. It is melted and recast into a hollow cylindrical pipe of 30 cm inner radius and thickness 5 cm. Find the length of the pipe.
A toy is in the form of a cone of radius 3.5 cm mounted on a hemisphere of same radius on its circular face. The total height of the toy is 15.5 cm. Find the total surface area of the toy.
How many terms of an A.P. 9, 17, 25, .... must be taken to give a sum of 636?
If the roots of the equation (a2 + b2) x2 – 2(ac + bd) x + (c2 + d2) = 0 are equal, prove that \\frac{a}{c} = \frac{b}{d})


