Question Three semicircles each of diameter 3 cm, a circle of diameter 4.5 cm and a semicircle of radius 4.5 cm are drawn in the given figure. Find the area of the shaded region.
Video Explanation
Explanatory Answer
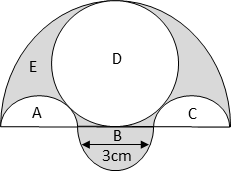
Area of the shaded region = area of semicircle E of radius 4.5 cm – (area of circle D of diameter 4.5cm + area of semicircle A of diameter 3cm)
Semicircles B and C cancel out each other. So there is no need to add B and subtract C.
Diameter of circle D = 4.5 = \\frac{9}{2}). Therefore, radius = \\frac{9}{4})
Diameter of semicircle A = 3 = Therefore, radius = \\frac{3}{2})
Area of semicircle E of radius \\frac{9}{2}) = \\frac {{{\pi }r}^{2}} {2}) = \\frac {\pi } {2}) \(\frac {9} {2}{)}^{2})= \\frac{81\pi}{8})
Area of circle D of radius \\frac{9}{4}) = (πr2) = π\(\frac {9} {4}{)}^{2}) = \\frac{81π}{16})
Area of semicircle A of radius \\frac{3}{2}) = \\frac {{{\pi }r}^{2}} {2}) = \\frac {\pi } {2}) \(\frac {3} {2}{)}^{2}) = \\frac{9\pi}{8})
Area of shaded region = \\frac{81\pi}{8}) - \\frac{81\pi}{16}) - \\frac{9\pi}{8})
= \\frac{162\pi - 81\pi - 18\pi}{16}) = \\frac{63\pi}{16})
Take π = \\frac{22}{7})
Therefore, \\frac{63\pi}{16}) = \\frac{63}{16}) × \\frac{22}{7}) = \\frac{9 * 11}{8}) = \\frac{99}{8}) = 12.375 cm2
.