Section A contains 4 questions of 1 mark each. Scroll down for explanatory answer and video solution to all four 1-mark questions.
The probability of selecting a rotten apple randomly from a heap of 900 apples is 0.18. What is the number of rotten apples in the heap?
If a tower 30 m high, casts a shadow 10\\sqrt3) m long on the ground, then what is the angle of elevation of the sun?
If the angle between two tangents drawn from an external point P to a circle of radius 'a' and centre 'O', is 60o, then find the length of OP.
What is the common difference of an A.P. in which a21 – a7 = 84?
Question 1: The probability of selecting a rotten apple randomly from a heap of 900 apples is 0.18. What is the number of rotten apples in the heap?
Video Explanation
Explanatory Answer
The probability of selecting a rotten apple = 0.18
Total number of apples = 900
The probability of selecting a rotten apple = \\frac{\text{Number of rotten apples}}{\text{Total number of apples}})
Let the number of rotten apples be x.
Therefore, \\frac{x}{900}) = 0.18
x = 900 × 0.18 = 162
Question 2: If a tower 30 m high, casts a shadow 10\\sqrt3) m long on the ground, then what is the angle of elevation of the sun?
Video Explanation
Explanatory Answer
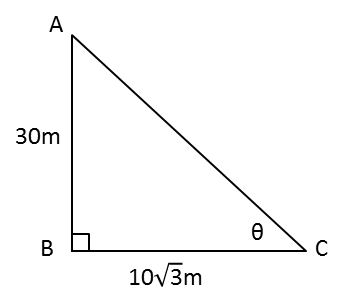
In the adjacent figure, AB is the tower and BC is the shadow.
θ is the angle of elevation.
tan θ = \\frac{\text{opposite side}}{\text{adjacent side}}) = \\frac{AB}{BC}) = \\frac{30}{10{\sqrt3}}) = \\frac{3}{\sqrt {3}} = {\sqrt {3}})
If tan θ = \\sqrt3), θ = 60°
The angle of elevation of the tower = 60°
Question 3: If the angle between two tangents drawn from an external point P to a circle of radius 'a' and centre 'O', is 60o, then find the length of OP.
Video Explanation
Explanatory Answer
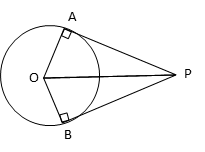
OAP and OBP are congruent triangles by RHS rule.
Explanation of the rule: OP is the common hypotenuse to both the right triangles OAP and OBP. One of the perpendicular sides of each of the triangles (OA and OB) are the radii to the circle. So, the third side of the two triangles, PA and PB will be equal. By SSS, the two triangles are congruent.
So, ∠APO = ∠BPO
Therefore, ∠APO = \\frac{∠APB}{2}) = \\frac{60}{2}) = 30o
In right triangle OAP
sin 30o = \\frac{\text{opposite side}}{\text{hypotenuse}}) = \\frac{OA}{OP})
OA is the radius = ‘a’
Therefore, sin 30o = \\frac{1}{2}) = \\frac{a}{OP})
Or the length of OP = 2a
Question 4: What is the common difference of an A.P. in which a21 – a7 = 84?
Video Explanation
Explanatory Answer
Key Data: a21 – a7 = 84. The numbers are in an AP.
For an AP, the nth term an = a1 + (n – 1)d, where a1 is the first term of the AP and 'd' is its common difference.
So, a21 = a1 + (21 – 1)d = a1 + 20d and
a7 = a1 + (7 – 1)d = a1 + 6d
a21 – a7 = a1 + 20d – (a1 + 6d) = 84
Or 14d = 84
d = \\frac{84}{14}) = 6
