Question In the given figure, two concentric circles with centre O have radii 21 cm and 42 cm. If ∠AOB = 60°, find the area of the shaded region. (Use π = \\frac{22}{7}))
Video Explanation
Explanatory Answer
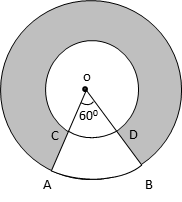
Radius of inner circle = 21cm
Radius of outer circle = 42cm
Area of the complete disc = area of outer circle – area of inner circle
= π(router)2 – π(rinner)2
But an arc AB subtending 60° is not shaded.
So, area of shaded region = \\frac{300}{360}) × area of complete disc
= \\frac{5}{6}) (π(42)2 - π(21)2)
= \\frac{5}{6}) π(422 – 212)
= \\frac{5}{6}) π[(42 + 21)(42 – 21)]
= \\frac{5}{6}) π(63 × 21)
= \\frac{5}{6}) × \\frac{22}{7}) (63 × 21)
= 55 × 63
= 3465 cm2