Question On a straight line passing through the foot of a tower, two points C and D are at distances of 4 m and 16 m from the foot respectively. If the angles of elevation from C and D of the top of the tower are complementary, then find the height of the tower.
Video Explanation
Explanatory Answer
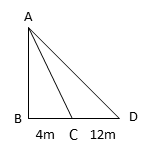
Let AB be the tower. Let AB = h
Points C and D are 4m and 16m from B
Let the angle of elevation from C, ∠BCA = θ
Because the angles of elevation from C and D are complementary, the angle of elevation from point D, ∠BDA = 90 – θ
tan θ = \\frac{\text{opposite side}}{\text{adjacent side}}) = \\frac{AB}{BC}) = \\frac{h}{4})
Similarly, tan(90 – θ) = \\frac{AB}{BD}) = \\frac{h}{16}) ....... (1)
But, tan (90 – θ) = cot θ
cot θ = \\frac{\text{adjacent side}}{\text{opposite side}}) = \\frac{BC}{AB}) = \\frac{4}{h}) ....... (2)
Equating tan (90 – θ) = \\frac{h}{16}) to cot θ = \\frac{4}{h}) we get \\frac{h}{16}) = \\frac{4}{h})
or h2 = 64
or h = 8.
The height of the tower is 8m.
