Question A toy is in the form of a cone of radius 3.5 cm mounted on a hemisphere of same radius on its circular face. The total height of the toy is 15.5 cm. Find the total surface area of the toy.
Video Explanation
Explanatory Answer
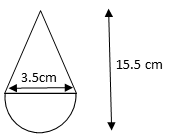
Total height of toy = 15.5 cm
Radius of hemisphere = 3.5cm = \\frac{7}{2}) cm
Therefore, height of conical portion of toy = 12 cm
Surface area of toy = lateral surface area of cone + surface area of hemisphere
= πrl + 2πr2, where ‘r’ is the radius (cone and hemisphere have the same radii) and ‘l’ the slant height of the cone.
Slant height of the cone, l = \\sqrt {{r}^{2}+{h}^{2}})
= \\sqrt {{\left ( {{\frac {7} {2}}} \right )}^{2}+{12}^{2}}) = \\sqrt {{\left ( {{\frac {7} {2}}} \right )}^{2}+{\left ( {{\frac {24} {2}}} \right )}^{2}})
= \\sqrt {\frac {{7}^{2}+{24}^{2}} {{2}^{2}}}) = \\sqrt {\frac {{}{25}^{2}} {{2}^{2}}}) = \\frac{25}{2}) cm
Surface area of cone = πrl = \\frac{22}{7}) × \\frac{7}{2}) × \\frac{25}{2}) = \\frac{275}{2})cm2
Surface area of hemisphere = 2πr2 = 2 × \\frac{22}{7}) × \\frac{7}{2}) × \\frac{7}{2}) = 77 cm2
Surface area of toy = \\frac{275}{2}) + 77 = 137.5 + 77 = 214.5 cm2
.