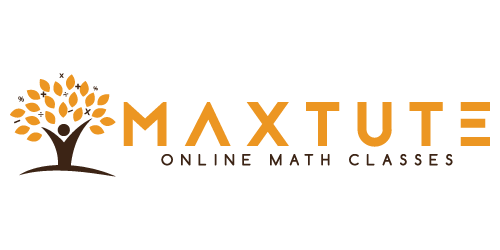Past CBSE Board Paper

Explanatory Answer

AC = 24cm
AB = 7cm
BC is the diameter to the circle.
Property: Angle in a semicircle is 90°
Therefore, ∠CAB = 90°
And CAB is a right triangle. And CB is the hypotenuse of the right triangle CAB.

Therefore, CB = \\sqrt {{CA}^{2}+{{AB}^{2}}}) = \\sqrt {{24}^{2}+{{7}^{2}}}) = \\sqrt {576+49}) = \\sqrt {625}) = 25

BC, the diameter of the circle = 25. So, radius of the circle = \\frac{25}{2})

Area of shaded region = area of circle – area of right triangle ABC – area of sector COD
= π \{\left ( {{\frac {25} {2}}} \right )}^{2}) - \\frac{1}{2}) × 24 × 7 - \\frac{90}{360})π \{\left ( {{\frac {25} {2}}} \right )}^{2})
= π \{\left ( {{\frac {25} {2}}} \right )}^{2}) - \\frac{1}{2}) × 24 × 7 - \\frac{1}{4})π \{\left ( {{\frac {25} {2}}} \right )}^{2})
= π \{\left ( {{\frac {25} {2}}} \right )}^{2}) - \\frac{1}{4})π \{\left ( {{\frac {25} {2}}} \right )}^{2}) - \\frac{1}{2}) × 24 × 7
= \\frac{3}{4}) π \{\left ( {{\frac {25} {2}}} \right )}^{2}) - \\frac{24 × 7}{2})
= \\frac{3}{4}) × \\frac{22}{7}) × \\frac{625}{4}) - \\frac{24 × 7}{2})
= \\frac{20625-4704}{56}) = \\frac{15921}{56}) = 284.3 (approx)

.