Question Prove that the tangents drawn at the end points of a chord of a circle make equal angles with the chord.
Video Explanation
Explanatory Answer
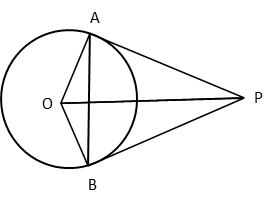Let ‘O’ be the centre of the circle.
PA and PB are two tangents drawn from point P.
AB is a chord to the circle.
OA and OB are radii to the circle.
∠OAP = ∠OBP = 90o because the angle between the tangent and the radius where the tangent meets the circle is a right angle.
Because OA and OB are radii to the circle, triangle AOB is isosceles.
Therefore, ∠OAB = ∠OBA.
Let the measures of ∠OAB = ∠OBA be θ.
∠PAB = ∠OAP - ∠OAB = 90 – θ
∠PBA = ∠OBP - ∠OBA = 90 – θ
i.e., ∠PAB = ∠PBA
The tangents PA and PB make equal angles with the chord AB.