Question A circle touches all the four sides of a quadrilateral ABCD. Prove that AB + CD = BC + DA.
Video Explanation
Explanatory Answer
If the circle touches all four sides of a quadrilateral ABCD, it is inscribed in the quadrilateral. The sides of the quadrilateral are tangents to the circle.
In the figure given below, let the points at which the circle touches the quadrilateral be P, Q, R, and S.
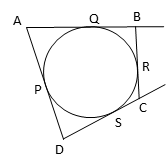
AP and AQ are equal tangents from external point A. Let the length of AP = AQ = ‘a’ units.
BQ and BR are equal tangents from point B. Let the length of BQ = BR = ‘b’ units.
CR and CS are equal tangents from point C. Let CR = CS = ‘c’ units.
DP and DS are equal tangents from point D. Let DP = DS = ‘d’ units.
AB + CD = AQ + QB + CS + SD
= a + b + c + d -----------------------------(1)
BC + DA = BR + RC + DP + AP
= b + c + d + a ----------------------------- (2)
(1) = (2), therefore, AB + CD = BC + DA
Property of circles: If a circle is inscribed in a quadrilateral, the measures of the sum of the opposite sides of the quadrilateral will be equal.
