Class 10 Math Sample Paper 2019 | Q20

This 2019 CBSE class 10 Maths 3 mark question is from Areas Related to Circles. This 3-mark question tests concept of computing area of a segment of a Circle. From the chapter Areas Related to Circles.

Question 20: Find the area of the minor segment of a circle of radius 42 cm, if length of the corresponding arc is 44 cm.

Video Explanation

Explanatory Answer | Question 20 | CBSE Sample Paper 2019

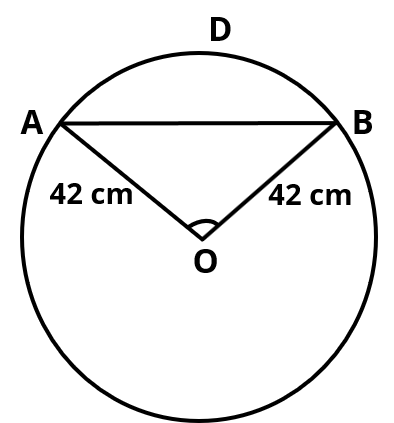
Area of the minor segment ADB = Area of sector OADB – Area of ΔOAB

Step 1: Find ∠AOB

Length of the arc of the minor segment = 44 cm
Length of arc that subtends an angle θ = \\frac{θ}{360}) × 2πr
\\frac{θ}{360}) × 2πr = \\frac{θ}{360}) × 2 × \\frac{22}{7}) × 42 = 44
θ = \\frac{44 × 7 × 360}{2 × 22 × 42}) = 60°

Step 2: Compute Area of sector OADB

Area of Sector = \\frac{θ}{360}) × πr²
= \\frac{60}{360}) × \\frac{22}{7}) × 42 × 42
= 924 cm²

Step 3: Compute Area of ΔOAB

OA = OB. So, ∠OAB = ∠OBA. Let ∠OBA = x
∠AOB = 60°
In a triangle sum of interior angles = 180°
60 + x + x = 180. Or x = 60°
So, ∠OAB is an equilateral triangle.

Area of ∠OAB = \\frac{√3}{4}) × a², where 'a' is the side of the triangle
Area of ∠OAB = \\frac{√3}{4}) × 42 × 42 = 441√3

Step 4: Compute Area of Minor Segment ADB

Area of the minor segment ADB = Area of sector OADB – Area of ΔOAB
= 924 - 441√3
= 21 (44 - 21√3) cm²