Class 10 Maths Sample Paper 2019 | Q18

This 2019 CBSE class 10 Maths 3 mark question is from Circles - Chords and Tangents. The core concept tested in this question is similarity of triangles.

Question 18: The radii of two concentric circles are 13 cm and 8 cm. AB is a diameter of the bigger circle and BD is a tangent to the smaller circle touching it at D and intersecting the larger circle at P on producing. Find the length of AP.

Video Explanation

Explanatory Answer | CBSE Sample Paper 2019 Question 18

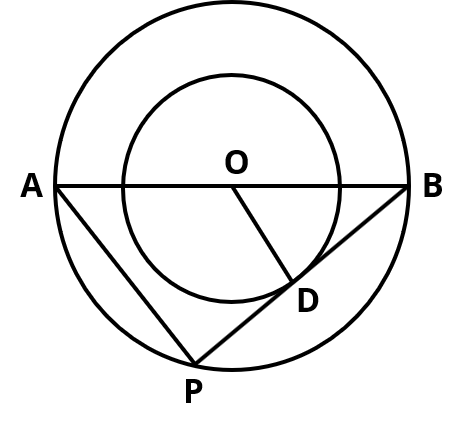
Given Data

OD is the radius of the smaller circle = 8 cm.
OB is the radius of the larger circle = 13 cm.
AB is the diameter of the bigger circle = 26 cm.

1. Angle in a semicircle is 90°. ∠APB = 90°
2. Tangent is perpendicular to the radius. OD ⊥ BP. ∠ODB = 90°

In ΔABP and ΔOBD, ∠B is common; ΔBDO and ΔBPA are equal.
Two angles of one triangle are respectively equal to two angles of another triangle. The two triangles are similar. ΔABP ~ ΔOBD
\\frac{\text{AB}}{\text{OB}}) = \\frac{\text{AP}}{\text{OD}})
\\frac{26}{13}) = \\frac{\text{AP}}{8})
AP = 26 × \\frac{8}{13}) = 16 cm